Определение параметров выборочного уравнения прямой линии регрессии по сгруппированным данным
Для определения параметров уравнения используем систему как и для несгруппированных данных:
Для применения этой системы воспользуемся тождеством:
С учетом тождеств систему можно переписать:
Решив систему, получим уравнение регрессии:
где
Выборочный коэффициент корреляции определяют из выражения:
Выборочный коэффициент корреляции На практике приняты следующие пределы качественной характеристики тесноты связи:
Пример 2.15. По данным корреляционной таблицы:
1. Вычислить коэффициент корреляции. 2. Найти уравнение регрессии 3. Вычислить групповые средние
4. По данным таблицы построить график линейной регрессии и нанести экспериментальные точки. Решение: 1 Вычисляем величины а)
б)
в)
г) коэффициент корреляции:
Так как 2. Вычислим коэффициент регрессии Искомое уравнение регрессии имеет вид:
3. Вычисляем групповые средние
Для контроля вычисляем значения
Результаты запишем в таблицу
4. Строим график линейной регрессии
 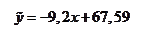 
Задания для самостоятельной работы: 1. Найти по уравнению регрессии
2. Найти уравнение регрессии
3. Найти уравнение регрессии
2.5.3. Однофакторный дисперсионный анализ Дисперсионным анализом называется статистический метод анализа результатов испытаний, цель которого – оценить влияние одного или нескольких качественных факторов на рассматриваемую величину Схему однофакторного дисперсионного анализа можно рассмотреть на примере исследования влияния различных факторов рекламы на прибыль предприятия. Если разделить виды рекламы на несколько групп (уровни фактора) и через одинаковые интервалы времени измерять прибыль, то результаты можно представить в виде таблицы:
Число измерений на каждом уровне считаем одинаковым и равным Общую среднюю можно получить как среднее арифметическое групповых средних:
На разброс прибыли относительно общей средней влияют как изменение уровня рассматриваемого фактора, так и случайные факторы. Для того чтобы учесть влияние данного фактора, общая выборочная дисперсия разбивается на две части, одна из которых называется факторной Для учёта этих составляющих вначале рассчитывается общая сумма квадратов отклонений вариант от общей средней:
И факторная сумма квадратов отклонений групповых средних от общей средней, которая и характеризует влияние данного фактора:
Последнее выражение Остаточная сумма квадратов отклонений получается как разность:
Для определения общей выборочной дисперсии необходимо
а для получения несмещённой общей выборочной дисперсии это выражение нужно умножить на
где Для несмещённой остаточной выборочной дисперсии число степеней свободы будет равно разности:
и выражение дисперсии примет вид:
С целью оценки влияния фактора на изменения рассматриваемого параметра рассчитывается величина:
Так как отклонение двух выборочных дисперсий Если Для расчёта
|

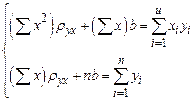
 (следствие из
(следствие из 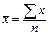 )
) (следствие из
(следствие из 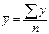 )
)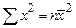 (следствие из
(следствие из 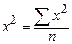 )
) (учтено, что когда пара чисел (x, y) наблюдалась
(учтено, что когда пара чисел (x, y) наблюдалась  раз).
раз).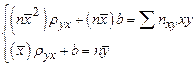
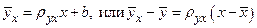 ,
, .
.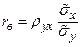 ; =>
; => 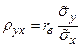 .
. .
.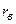 является оценкой коэффициента корреляции r генеральной совокупности и поэтому служит для измерения линейной связи.
является оценкой коэффициента корреляции r генеральной совокупности и поэтому служит для измерения линейной связи. - связь между X и Y отсутствует или не является линейной даже приближенно;
- связь между X и Y отсутствует или не является линейной даже приближенно;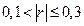 - связь слабая;
- связь слабая; - связь умеренная;
- связь умеренная; - связь заметная;
- связь заметная; - связь очень высокая;
- связь очень высокая; - связь между X и Y можно считать функциональной.
- связь между X и Y можно считать функциональной.
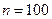
 .
. и для контроля вычислить значение
и для контроля вычислить значение 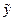 (по уравнению регрессии в тех же точках), результаты запишем в таблицу:
(по уравнению регрессии в тех же точках), результаты запишем в таблицу: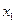

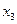
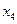
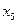
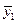


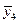



 , а также
, а также 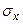 и
и  по формулам:
по формулам: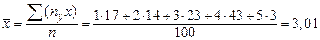 ;
;  ;
; ;
; ;
;  .
.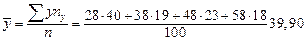 4;
4; 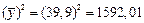 ;
; ;
; ;
; 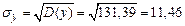 ;.
;.
 ;
; 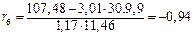 .
.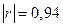 , то между величинами X и Y имеется очень высокая линейная корреляционная связь.
, то между величинами X и Y имеется очень высокая линейная корреляционная связь. ;
; 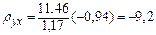 .
. ;
;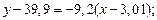

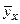 признака
признака 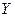 при фиксированном значении
при фиксированном значении 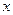 по формулам
по формулам 


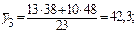


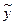 по уравнению регрессии в тех же точках:
по уравнению регрессии в тех же точках: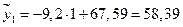



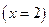




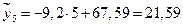
 .
. 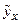
 и наносим экспериментальные точки
и наносим экспериментальные точки  .
.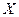 на
на 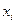 yi
yi
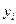





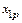


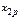



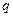

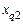
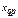



 .
.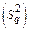 , а вторая - остаточной
, а вторая - остаточной 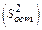 .
.
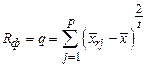
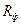 получено путём замены каждой варианты в выражении
получено путём замены каждой варианты в выражении  - групповой средней для данного фактора.
- групповой средней для данного фактора.
 разделить на число измерений
разделить на число измерений  :
:
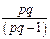 :
:
 - число отклонений свободы несмещённой факторной выборочной дисперсии.
- число отклонений свободы несмещённой факторной выборочной дисперсии.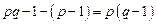 ,
, .
.
 и
и  распределено по закону Фишера-Снедекора, то полученное значение
распределено по закону Фишера-Снедекора, то полученное значение  сравнивают со значением функции распределения
сравнивают со значением функции распределения  в критической точке
в критической точке  , соответствующей выбранному уровню значимости
, соответствующей выбранному уровню значимости 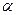 .
. то фактор оказывает существенные воздействия и его следует учитывать, в противном случае он оказывает незначительное влияние, которым можно пренебречь.
то фактор оказывает существенные воздействия и его следует учитывать, в противном случае он оказывает незначительное влияние, которым можно пренебречь. и
и 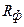 могут быть использованы также формулы:
могут быть использованы также формулы:



