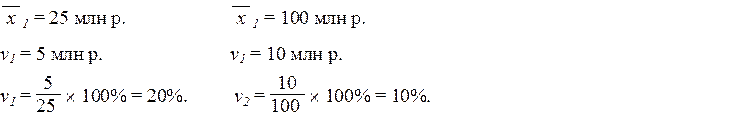Свойства дисперсии
1. Если все варианты увеличить или уменьшить в k раз, то дисперсия увеличится или уменьшится в k раз. 2. Увеличение или уменьшение вариантов на одну и ту же величину не меняет дисперсию. 3. Если все частоты увеличить или уменьшить в несколько раз, то дисперсия не изменится. 4. Дисперсия относительно средней арифметической равна дисперсии относительно произвольной постоянной без квадрата разности между средней арифметической и этой постоянной.
5. Дисперсия равна средней арифметической квадратов вариантов без квадрата средней арифметической. Если в 4-м свойстве дисперсии с=0, то имеем формулу:
Дисперсию можно рассчитать тремя способами. Пример: определить дисперсию затрат на 1 руб. реализованных путевок по 30 пансионатам:
Решить можно тремя способами, используя свойства дисперсии. Способ 1.
.
Способ 2.
За число «с» принимается варианта, расположенная в середине ряда распределения, или варианта, имеющая наибольшую частоту (в нашем случае с=80).
Способ 3..
Г. Среднее квадратическое отклонение ( s ) – это арифметическое значение корня квадратного из дисперсии:
Отклонение затрат на 1 руб. реализованных путевок от среднего значения составляет 7,48 коп. Хотелось бы отметить, что отношение среднего квадратического отклонения к среднему линейному приблизительно равно 1,2:
Так, при s =7,48 прогнозируемое значение d=6,23, а реальное (рассчитанное по исходным данным) d=6,00. Д. Коэффициент вариации ( n ) – это отношение среднего квадратического отклонения к средней арифметической, выраженное в процентах:
Он показывает долю колебания признака от средней арифметической. Применяется для сравнения вариаций признака в различных совокупностях и для характеристики колебания различных признаков в одной совокупности. Коэффициент вариации характеризует также степень однородности совокупности и качества средних величин, т.е. если коэффициент вариации от 0 до 20 %, то совокупность – однородная, если коэффициент вариации – от 20 до 50% – совокупность средней однородности, т.е. необходимо осторожно использовать среднюю, если свыше 50% – совокупность неоднородна, и средней нельзя пользоваться для прогнозирования перспективных показателей признака. Целесообразно расчет каждой средней величины дополнять расчетом коэффициента вариации для характеристики степени однородности совокупности и оценки качества средней величины. В нашем примере коэффициент вариации составит:
Это означает, что совокупность предприятий по уровню затрат на 1 руб. проданных путевок является однородной. Средней величиной пользоваться можно. Пример: В течение одного квартала производство продукции в среднем за декаду на заводе № 1 составило 25 млн руб. при n=5 млн руб., на заводе № 2 – соответственно 100 млн руб. и 10 млн руб. Определить, какой завод работал ритмичнее, т.е. с меньшей колеблемостью выпуска продукции по дням? Для решения задачи необходимо найти коэффициенты вариации выпуска продукции по двум заводам в отдельности и сравнить их.
Второе предприятие работало ритмичнее, так как
|

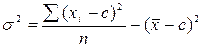 (5.6)
(5.6) (5.7)
(5.7) (5.8)
(5.8) (5.9)
(5.9)
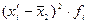




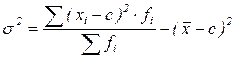 – способ моментов
– способ моментов .
.

 (5.10)
(5.10)
 (5.11)
(5.11)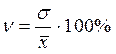 (5.12)
(5.12)