Теоретические сведения. Движения спортсмена в физических упражнениях целенаправленны и выполняются в соответствии с программой
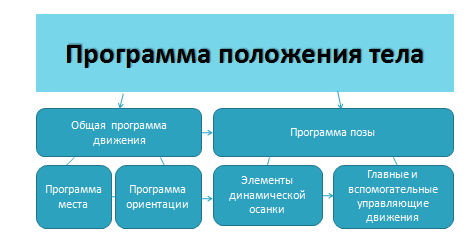
Движения спортсмена в физических упражнениях целенаправленны и выполняются в соответствии с программой, называемой программой положения тела (см. рис. 1.2.1). . Рис. 1.2.1
Составной частью программы положения тела является программа места, описывающая закономерность, в соответствии с которой с течением времени перемещается ОЦТ тела при выполнении упражнения ОЦТ тела – это точка на теле спортсмена или вне его, к которой приложена равнодействующая сила тяжести всех звеньев тела. Важной характеристикой программы места является траектория ОЦТ тела – линия, представляющая собой воображаемый след, который оставляет ОЦТ тела, перемещающийся в ходе физического упражнения. Каждое звено тела спортсмена имеет свой собственный центр тяжести (ЦТ), который расположен на продольной оси ближе к проксимальному (как правило, более массивному) концу звена. Например, ЦТ бедра располагается на его продольной оси с некоторым смещением от середины бедра в сторону тазобедренного сустава, ЦТ туловища – в сторону шейного отдела позвоночника. Положение ОЦТ системы, состоящей из нескольких тел (звеньев) можно определить аналитически. Для двух жестко связанных между собой звеньев положение ОЦТ определяется следующим образом. Рис. 1.2.2 На рис. 1.2.2 определена схема, изображающая систему из двух звеньев в виде шаров, имеющих веса p1 и p2, приложенные к их центрам. Звенья жестко соединены друг с другом тонким невесовым стержнем. В плоской прямоугольной системе координат x Оy центры звеньев имеют координаты: звено с весом p1 – координаты (x1, y1) а звено с весом p2 – координаты (x2, y2). В этом случае ОЦТ системы двух этих звеньев будет находиться в некоторой точке с координатами (Х, Y). Если в точку расположения ОЦТ подвести опору и приложить силу F, направленную противоположно силам тяжести звеньев p1 и p2 и равную по величине их сумме p1 + p2, то система окажется в равновесии, при котором имеет место равенство моментов сил, один из которых вращает рассматриваемую систему по часовой стрелке, а второй – в противоположном направлении:
p1(Х – x1) = p2(x2 – Х). (1.2.1)
Пользуясь выражением (1.2.1), определим координату Х ОЦТ системы двух звеньев:
p1 Х – p1x1 = p2x2 – p2 Х p1 Х + p2 Х = p1x1 + p2x2 X (p1 + p2) = p1x1 + p2x2
Формула (1.2.2) позволяет аналитически определить положение ОЦТ системы из двух жестко связанных между собой звеньев. Для системы, состоящей из n звеньев, координата Х будет определяться по формуле:
Х
где Х – координата ОЦТ системы из n звеньев, pi – вес i-го звена; xi – координата ЦТ i-го звена; Р – вес всех вместе взятых звеньев системы. Если систему из двух звеньев, размещенную в системе координат x O y (см. рис. 1.2.2), повернуть вместе с этой системой координат по часовой стрелке или против нее на 90º, то очевидно, что положение ОЦТ на соединяющем звенья стержне не изменится. В этом случае, по аналогии с формулой (1.2.3), координата Y ОЦТ системы, состоящей из n жестко связанных друг с другом звеньев, определяется по формуле:
Y
Пользуясь формулами (1.2.3) и (1.2.4), можно рассчитать координаты Х и Y ОЦТ тела спортсмена во всех позах, предоставленных видеосъемкой и отображающих отдельные моменты исследуемой фазы физического упражнения. Используя реализованные в специальных компьютерных программах, в частности в Excel, математические методы построения кривых по точкам, заданным своими координатами, можно получить с высокой степенью точности приближенную траекторию ОЦТ тела в рассматриваемой фазе физического упражнения.
|

 (1.2.2)
(1.2.2)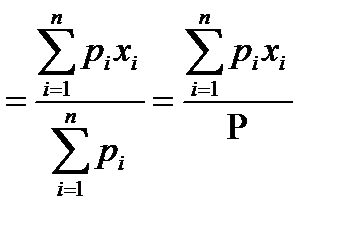 , (1.2.3)
, (1.2.3) . (1.2.4)
. (1.2.4)


