Матрица сетевых корреспонденции

Векторное распределение пассажиропотока 30% - 30% - 40%

 

Цель данной работы заключается в выборе наиболее оптимальной транспортной сети для заданного района города.

 

 

После определения нагрузки на транспортную сеть становится возможным построение матрицы сетевых корреспонденции.

Матрица 1

	-	9,12,6 4100	9,5,11,10 3900	9,5,8,7 4000	9 3000	9,12 4500	9,5,8 3500	9,5** 5000	4460	9,5,11 3000	9,5 * 4000	9 1000
	6,12,9 2000	-	8,7,4,10 2750	8,7 2750	8,** 5000	2003	8 2750	3007	6,12 2000	8,7,4 2750	8,5 2000	6 3000
	10,11,5.9 3000	10,4,7,8 3000	-	10 1000	10,11 3000	10,4,7,8,2 3000	10,4 3000	10,4,7 3000	10,11,5 3000	3720	10 3000	10,4,7,8,2,6 * 5000
	7,8,5,9	7,8 1000	10 1000	-	7,8 2500	7,8,2 3000	1000	7 1500	7,8,5 2500	1280	10 3000	7,8,5,9** 5500
	9 3000	8 1000	*11,10 5000	8,7 500	-	8,2 4000	8 500	1083	948	11 4000	444	9 3000
	12,9 1000	2000	2,8,7,4,10 * 5374	2,8,7 2000	2,8 2000	-	2,8 2000	2 1500	12* 4500	2,8,7,4 * 4500	2,8,5 4000	3500
	8,5,9 * 4230	8 1600	4,10 2000	1200	8 1600	8,2 2000	-	1200	8,5 1600	4 2000	8,5 1200	8,5,9 1600
	5,9 4000	7000	7,4,10* 5521	7 2000	521	2 7028	2000	-	5 1000	7,4 1000	5 1000	5,9 4000
	** 19424	12,6 * 5568	5,11,10 2568	5,8,7 2000	2000	12 4500	5,8 3000	5 1000	-	5,11 2500	5 1500	4500
	11,5,9	4,7,9 4000	** 12747	1996	11	4,7,8,2 4000	4 3000	4,7 4000	11,5 2000	-	747	11,5,9 4000
	5,9	5,8 3500	10 3000	10* 4500	3750	5,8,2 ** 7770	5,8 * 5250	5 3000	5 3750	3000	-	5,9 3750
	9	6	6,2,8,7,4,10 * 9000	9,5,8,7 3000	9 1000	3000	9,5,8 2000	9.5 1500	3000	11,5,9 2500	9-5 2000	-

 

В матрице методом двойного предпочтения выбираются три наибольших значения пассажиропотока и определяется максимальная нагрузка пассажиропотока: Q_max = (19424+12747+7770) / 3 = 13222 пасс./ч.

Это говорит о том, что вид применяемого городского транспорта –

Скоростной трамвай (\/_с = 27 км/ч, g_н= 300 пассажиров).

 

Граф времени

Следующие преобразования определяются целевой функцией решаемой задачи. Так как целью работы является поиск маршрутной сети ГПТ, обеспечивающий минимальные затраты жителей города на передвижение, то следовательно, целевой функцией является время.

Зная значение средней скорости сообщения, реализуемое выбранной транспортной системы, делим протяженность «ребра» модели на скорость сообщения выбранного вида ГПТ. В результате расчета получаем среднее время движения транспортного средства на каждом звене (ребре) транспортной модели города. Заменив параметры расстояния соответственно на время проезда по каждому звену исходного графа, получаем граф времени или транспортную модель города, обслуживаемую выбранным видом или видами городского транспорта.

Построение базового варианта маршрутной сети

 

Для построения базового варианта маршрутной сети по матрице сетевых корреспонденции в таблицу выписываются сквозные маршруты, начиная с самого длинного (по убывающей).

Время ожидания автобуса t_ож рассчитывается по формуле:

, где

g_н - номинальная пассажировместимость (пассажиров);

Q_max - максимальное значение пассажиропотока из матрицы сетевых корреспонденции (пасс./ч.).

Время пересадки на промежуточных пунктах t_пер берется из таблицы:

 

Табл.2

 

№ п/п

tпер

 

Базовый вариант маршрутной сети:

 

Табл. 3

Маршрут	tож, мин.	tпер, мин.	±
3-10-4-7-8-2-6-12			+
12-6-2-8-7-4-10-3			+
3-10-4-7-8-2-6	1,67		+
6-2-8-7-4-10-3	1,67		+
1-9-5-11-10-3	2,3
3-10-11-5-9-1	2,3
1-9-5-8-7-4	2,25
4-7-8-5-9-1	2,25
2-8-7-4-10-3
3-10-4-7-8-2
4-7-8-5-9-12	1,63		+
12-9-5-8-7-4	1,63		+
6-2-8-7-4-10			+
10-4-7-8-2-6			+
1-9-12-6-2	2,2
2-6-12-9-1	2,2
1-9-5-8-7	2,1
7-8-5-9-1	2,1
1-9-5-11-10	2,25
10-11-5-9-1	2,25
2-8-7-4-10	2,25
10-4-7-9-2	2,25
3-10-4-7-8	1,6		+
8-7-4-10-3	1,6		+
3-10-11-5-9
9-5-11-10-3
4-7-8-2-6
6-2-8-7-4
4-7-8-5-9	3,6
9-5-8-7-4	3,6
6-2-8-5-11	1,15		+
11-5-8-2-6	1,15		+
7-8-5-9-12	4,5
12-9-5-8-7	4,5
10-11-5-9-12	2,4
12-11-5-9-10	2,4
1-9-12-6			+
6-12-9-1			+
1-9-5-8	1,8		+
8-5-9-1	1,8		+
1-9-5-11	2,25
11-5-9-1	2,25
2-8-7-4	3,27
4-7-8-2	3,27
2-6-12-9	1,61		+
9-12-6-2	1,61		+
2-8-5-11	2,57
11-5-8-2	2,57
3-10-11-5
5-11-10-3
3-10-4-7
7-4-10-3
4-7-8-5	3,6
5-8-7-4	3,6
5-8-2-6	2,25
6-2-8-5	2,25
6-2-8-7	4,5
7-8-2-6	4,5
7-8-5-9
9-5-8-7
7-8-5-11	2,1
11-5-8-7	2,1
8-7-4-10	2,25
10-4-7-8	2,25
8-5-9-12	2,25
12-9-5-8	2,25
9-5-11-10	3,6
10-11-5-9	3,6
11-5-9-12	2,4
12-9-5-11	2,4
1-9-5
5-9-1
1-9-12
12-9-1
2-8-5	1,8		+
5-8-2	1,8		+
2-8-7	3,2
7-8-2	3,2
2-6-12
12-6-2
3-10-4
4-10-3
3-10-11			+
11-10-3			+
4-7-8	4,5
8-7-4	4,5
4-10-11			+
11-10-4			+
5-8-7	5,6
7-8-5	5,6
5-11-10	2,25
10-11-5	2,25
5-9-12
12-9-5
6-2-8	1,28		+
8-2-6	1,28		+
6-12-9			+
9-12-6			+
7-4-10			+
10-4-7			+
8-5-9
9-5-8
8-5-11
11-5-8
9-5-11	2,4
11-5-9	2,4

При формировании базового варианта маршрутной сети, маршруты, в которых t_ож ≤ t_пер, не берутся во внимание (т.к. пассажиру удобнее подождать автобус, чем ехать с пересадкой). Из оставшихся выбираются такие, чтобы их количество было минимально, но они охватывали все пункты графа.

В случае необходимости, отдельные вершины, не связанные выбранными ранее сквозными маршрутами, следует связать с маршрутной сетью участковыми маршрутами. Если возникает возможность использования нескольких участковых маршрутов то в маршрутную сеть города включается тот маршрут который по расчету должен работать с наименьшим интервалом движения.

 

В данной работе базовый вариант маршрутной сети города формируется из трёх сквозных маршрутов:

 

Маршрут №1 3-10-4-7-8-2-6-12

Маршрут №2 1-9-5-8

Маршрут №3 3-10-11

 

Первый вариант маршрутной сети города представлен на Рис. 7.1

 

Выбор оптимального варианта маршрутной сети

Определение значения целевой функции базового варианта маршрутной сети

Матрица 2

-

-

-

-

-

-

-

-

-

-

-

-

Суммарные затраты времени поездок пассажиров города (величина целевой функции задачи оптимизации) для базового варианта маршрутной сети составит:

ΣT₁= 2475104 мин/ч. «пик».

С целью поиска оптимального решения, разработаем второй вариант маршрутной сети города. Для этого рассмотрим свободные связи (ребра) транспортной модели города. Свободной связью является ребро графа города не задействованное для работы маршрутов, включенных в первый вариант маршрутной сети. Для второго варианта необходимо увеличить количество маршрутов за счет введения в маршрутную сеть нового маршрута. В качестве нового маршрута может быть использован только участковый маршрут.

Формируем второй вариант маршрутной сети города, добавляя участковый маршрут 11-5: Получим новую маршрутную сеть состоящую из трёх сквозных и одного участкового маршрутов. Второй вариант маршрутной сети города представлен на Рис. 7.2

 

Маршрут №1 3-10-4-7-8-2-6-12

Маршрут №2 1-9-5-8

Маршрут №3 3-10-11

Маршрут №4 11-5

 

 

Матрица 3

-

-

-

-

-

-

-

-

-

-

-

-

Суммарные затраты времени поездок пассажиров города (величина целевой функции задачи оптимизации) для базового варианта маршрутной сети составит:

ΣT₁= 2370444 мин/ч. «пик»

Формируем третий вариант маршрутной сети города, добавляя участковый маршрут 9-12: Получим новую маршрутную сеть состоящую из трёх сквозных и двух участковых маршрутов. Третий вариант маршрутной сети города представлен на Рис. 7.3

 

Маршрут №1 3-10-4-7-8-2-6-12
Маршрут №2 1-9-5-8
Маршрут №3 3-10-11
Маршрут №4 11-5
Маршрут №5 9-12

Матрица 4

-

-

-

-

-

-

-

-

-

-

-

-

Суммарные затраты времени поездок пассажиров города (величина целевой функции задачи оптимизации) для базового варианта маршрутной сети составит:

ΣT₁= 2285074 мин/ч. «пик»

 

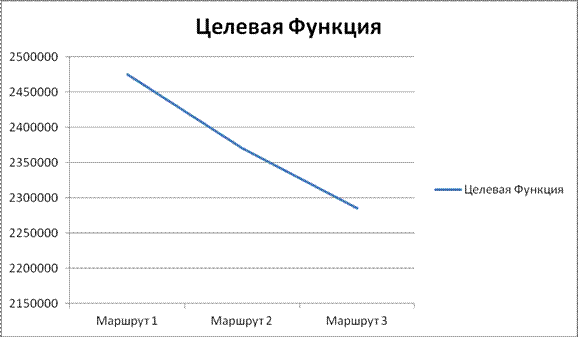
Изобразим результаты расчетов графически и построим график изменения целевой функции ΣT_i на каждому варианту маршрутной сети города, начиная с базового.

 

Вывод: Следует считать поиск оптимального варианта маршрутной сети для выбранного вида ГПТ оконченным. Наиболее рациональным следует считать 3ой вариант маршрутной сети, так как он отличается от второго более чем на 4,2%.

Дальше(после третьего варианта) мы транспортную сеть не оптимизируем, так как не осталось свободных связей