Постановка задачи. Любое сложное движение абсолютно твердого тела можно представить в виде суммы двух простых движений: вращательного и поступательного
Любое сложное движение абсолютно твердого тела можно представить в виде суммы двух простых движений: вращательного и поступательного. Сложное движение удобно моделировать на приборе, называемом маятником Максвелла. Маятник Максвелла представляет собой диск, неподвижно закрепленный на тонком валу, ось которого проходит через центр инерции. Маятник подвешивается к штативу на двух нитях, закрепленных на концах вала симметрично относительно диска. При вращении вала нити наматываются на вал маятника или разматываются, тем самым обеспечивая поступательное перемещение маятника вверх вниз. Если, намотав нить на вал, поднять маятник на некоторую высоту h и отпустить его, то он начнет совершать возвратно-поступательное движение под действием сил тяжести и сил натяжения нитей. При опускании диска вниз нити разматываются до полной длины. Поступательное движение маятника в этот момент прекращается, но он продолжает вращение в том же направлении и наматывает нити на вал, вследствие чего он поднимается вверх, замедляя при этом свое вращение. Дойдя до верхней точки, маятник останавливается. После чего снова опускается вниз. На рис. 1 показана схема сил, действующих на вал. Движение маятника осуществляется под действием силы тяжести mg, приложенной в центре инерции и силы натяжения нитей N, действующей по касательной к валу и направленной вертикально вверх. Они образуют пару сил с плечом, равным
Рис. 1 Под действием пары сил с постоянным моментом маятник совершает равноускоренное вращение в направлении, показанном стрелкой, и равномерно ускоренное опускание с ускорением
Кинетическая энергия маятника в каждый момент времени складывается из энергии поступательного и вращательного движений.
(где Из формул (1) и (2) получим:
Согласно закону сохранения механической энергии при движении в поле силы тяжести кинетическая энергия маятника, который опускается с высоты h, равна его потенциальной энергии на этой высоте
Рассматривая нити как нерастяжимые, считаем, что линейная скорость точек на ободе вала равна линейной скорости опускания центра инерции маятника. Линейную скорость опускания маятника определим из закона равноускоренного движения:
(где Так как при Подставив это значение линейной скорости в (4), запишем формулу перехода потенциальной энергии маятника в кинетическую в виде:
Решив равенство (5) относительно
(где h – высота, с которой опускается маятник, t – время опускания). Измерение пройденного маятником пути осуществляется мерной линейкой, нанесенной на стойке прибора, показанного на рис. 2, а время движения осуществляется автоматическим счетчиком, который включается электромагнитным датчиком П в момент начала опускания маятника и выключается фотоэлектрическим датчиком Ф в момент полного разматывания нитей (при этом ось маятника на мгновение останавливается). Масса маятника mуказывается в паспорте прибора и приводится на стенде лаборатории. Диаметр вала d измеряется штангенциркулем. К прибору прилагается набор колец с различной массой, которые плотно надеваются на диск маятника, что позволяет рассматривать диск с одетым кольцом как маятник Максвелла с другой массой Примечание: измерение времени опускания маятника может выполняться с помощью секундомера.
Рис. 2
|

 (где
(где 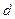 - диаметр вала).
- диаметр вала).
 . При этом угловая скорость
. При этом угловая скорость  вращения диска вала связаны соотношением:
вращения диска вала связаны соотношением: ,(где
,(где 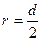 ),откуда
),откуда  (1)
(1)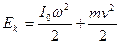 (2)
(2)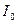 - момент инерции маятника относительно оси, проходящей через центр инерции, m - масса маятника).
- момент инерции маятника относительно оси, проходящей через центр инерции, m - масса маятника). (3)
(3) . Подставив в формулу (3) вместо
. Подставив в формулу (3) вместо  равную ей
равную ей  , получим:
, получим: (4)
(4) , откуда при
, откуда при 

 , линейная скорость
, линейная скорость  , то, заменив в этом равенстве
, то, заменив в этом равенстве  ,получим:
,получим: 
 (5)
(5) (6)
(6) и другим диаметром D. Измерив момент инерции
и другим диаметром D. Измерив момент инерции 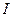 такого маятника, используя ту же расчетную формулу (6), момент инерции кольца
такого маятника, используя ту же расчетную формулу (6), момент инерции кольца 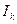 найдем как разность
найдем как разность  .
.



