Ответ :Вариант №6 1. Диск радиусом R =10 см вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением ϕ= A+Bt+Ct 2 +Dt 3 (B =1 рад/с, С =1 рад/с2, D =1 рад/с3). Определить для точек на ободе колеса к концу второй секунды после начала движения: 1) тангенциальное ускорение а к; 2) нормальное ускорение аn; 3) полное ускорение а. Дано: Решение: φ= D=1рад B=1рад/с аn= С=1рад/ R=10см=0,1м t=2c Найдем угловую скорость и нормальное а к, аn, а-? ускорение в указанный момент времени:
Выполним подстановку: 2) Для нахождения
Выполним подстановку данных в условия задачи: 3) Полное ускорение
Ответ: 2. Самолет описывает петлю Нестерова радиусом 80 м. Какова должна быть наименьшая скорость самолета, чтобы летчик не оторвался от сиденья в верхней части петли?
Дано: Решение: R=80 м Так как летчик вместе с самолетом движется по окружности,то в
Эти силы сообщают самолету необходимое для вращения центростремительное ускорение.Следовательно,в общем случае:
направлена в ту же сторону,что и сила тяжести, и, следовательно,пилот будет прижат к сидению. При Отсюда Выполним подстановку и проверку размерности:
Ответ: 3. Зависимость потенциальной энергии частицы в центральном силовом поле от расстояния r до центра поля задается выражением П (r) = , где А и В — положительные постоянные. Определить значение r 0, соответствующее равновесному положению частицы. Является ли это положение положением устойчивого равновесия? Дано: Решение:
Ответ:. 4. Определить относительное удлинение алюминиевого стержня, если при его растяжении затрачена работа 62,1 Дж. Длина стержня 2 м, площадь поперечного сечения 1 мм2, модуль Юнга для алюминия E =69 ГПа. Дано: Решение: A=62.1 Дж l=2 м S=1м E=69 ГПа=69
5. Определить, в какой точке (считая от Земли) на прямой, соединяющей центры Земли и Луны, напряженность поля тяготения равна нулю. Расстояние между центрами Земли и Луны равно R, масса Земли в 81 раз больше массы Луны.
 =0,
 ,
Ответ: х=0,9R 6. Сопло фонтана, дающего вертикальную струю высотой H = 5 м, имеет форму усеченного конуса, сужающегося вверх. Диаметр нижнего сечения d 1 = 6 см, верхнего — d 2 = 2 см. Высота сопла h = 1 м. Пренебрегая сопротивлением воздуха в струе и сопротивлением в сопле, определить: 1) расход воды в 1 с, подаваемой фонтаном; 2) разность Δ р давления в нижнем сечении и атмосферного давления. Плотность воды ρ =1 г/см3. Дано: Решение: H=5 м В потоке жидкости в сопле выделим два горизонтальных
h=1 м любое сечение сопла.Скорость воды, протекающей через
Тогда
Запишем уравнение Бернулли для потока жидкости в сопле фонтана между сечениями (1) и (2):
где
Для определения скорости воды в сечении (1) воспользуемся уравнением неразрывности струи:
Объединяя записанные равенства, получаем ответ:
Ответ:
7. Определить скорость, при которой релятивистский импульс частицы превышает ее ньютоновский импульс в пять раз. Решение: Классический (ньютоновский) импульс определяется по формуле: Релятивистский импульс определяется по формуле: Так по условию релятивистский импульс частицы превышает ньютоновский в 5 раз,тогда запишем:
,следовательно, искомая скорость движения релятивистской частицы
Ответ: v=0.98с.
8. Используя закон о распределении молекул идеального газа по скоростям, найти закон, выражающий распределение молекул по относительным скоростям и (u = v / v B).
Дано: Решение:
|
+ 
1) Воспользуемся Формулами связи угловой
скорости ω и нормального ускорения:
,
где угловая скорость по определению равна:
.
+ 
=B+2Ct+3D 
.
= 
.
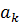воспользуемся соотношением между ней и угловым ускорением 
: 
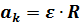, где 
по определению. Найдем угловое ускорение 
в указанный момент времени:
=1.4 
так как численные значения 
нам уже известны,то просто выполним подстановку:
=28.9м/ 
=1.4м/ 
.
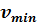=? в вершине петли на пилота действует сила тяжести mg с сила реакции опоры N со стороны сиденья,направленная вниз.
=mg+N. При достаточно большой скорости самолета
и N 
,т.е. N
= mg пилот перестанет давить на сидение. Наконец,при настолько малой скорости,что 
, сила N<0. В этом случае летчик повиснет на ремнях(если они у него есть). Таким образом, требуемое значение скорости определяется неравенством 
= 
.
= 
=28 
); 
= 
.
=100,8 км/ч.
- 
,
В равновесном положении F=0
,
,
, 
,
= 
, 
.
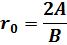
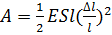Па
Ответ: 
, 
, 
,
, 
, 
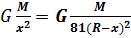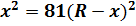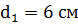сечения: нижнее (1) и верхнее(2).Расход воды 
равен
объему жидкости, протекающей за единицу времени через
=1 
сечение (2) легко найти по высоте подъема в поле силы
тяжести:
.
.
,
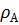-атмосферное давление.Из последнего уравнения находим избыточное давление:
.
.
= 58,3кПа
; 
58,3кПа
.
.
;
;
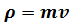с
, 
, 
, 
,
.
