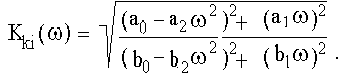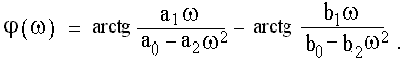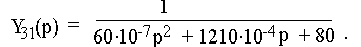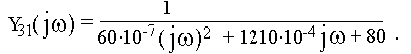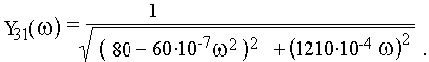Расчет комплексной передаточной характеристики цепи
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Справочная книга для проектирования электрического освещения / Под ред. Г. М. Кнорринга. Л.: Энергия, 1976.-384 с. ил. 2. Тищенко Г. А. Осветительные установки: Учебник для учащихся специальности “Электроосветительные приборы и установки”. – М.: Высшая школа, 1984. – 247 с. 3. Справочная книга по светотехнике / Под ред. Ю. В. Айзенберга. – М.: Энергоиздат, 1983, – 489 с. 4. СниП 23-05-95. Естественное и искусственное освещение. Нормы проектирования. – М.: Стройиздат, 1980.
Расчет комплексной передаточной характеристики цепи Рассмотрим идеализированную линейную цепь, не содержащую независимых источников тока и напряжения (рис.39).
Рис. 39 Операторной, или обобщенной частотной характеристикой Hki(p) линейной цепи называется отношение операторного изображения отклика цепи Y(p) к операторному изображению внешнего воздействия X(p)при нулевых начальных условиях:
Операторная характеристика цепи определяется только видом цепи и параметрами входящих в неё элементов. Операторные характеристики делятся на входные и передаточные. В зависимости от того, какая величина выступает в качестве внешнего воздействия, а какая в качестве отклика различают: 1. Операторное входное сопротивление
2. Операторную входную проводимость
3. Операторный коэффициент передачи по напряжению
4. Операторный коэффициент передачи по току
Операторное передаточное сопротивление
Операторную передаточную проводимость
Для расчета обобщенной характеристики цепи можно применить любые известные методы, например, метод контурных токов, метод узловых напряжений, метод эквивалентного генератора и др. Если сложная цепь содержит только один источник Еi(p), включенный в i-ом контуре, то контурный ток, создаваемый при этом в другом k- ом контуре
где
-алгебраическое дополнение элемента в операторной форме
Минор Следовательно
Поскольку представляют собой полиномы от собственных и взаимных операторных сопротивлений независимых контуров цепи, а сопротивления являются рациональными функциями р с вещественными коэффициентами, любая операторная характеристика линейной цепи Hki(p) также является рациональной функцией р с вещественными коэффициентами, т.е. может быть представлена в виде отношения двух полиномов
Для перехода от операторной характеристики цепи к её комплексной частотной характеристике (КЧХ) необходимо заменить р на jw, т. е. КЧХ есть частный случай обобщенной частотной характеристики при р = jw. Таким образом, комплексную частотную характеристику можно представить в виде отношения двух полиномов по степеням jw. Порядок полинома знаменателя равен порядку цепи, порядок числителя может быть ниже. Например, для цепи второго порядка
Как и всякое комплексное число, КЧХ может быть представлена в показательной или в алгебраической формах. Следовательно, и комплексный коэффициент передачи по напряжению можно представить в виде
где
j(w) - фазочастотная характеристика (ФЧХ) цепи.
Аналогично можно представить комплексную передаточную проводимость:
Известно, что модуль дроби определяется как отношение модулей числителя и знаменателя, поэтому амплитудно-частотная характеристика
Аргумент дроби равен разности аргументов числителя и знаменателя, поэтому фазочастотная характеристика
Пример 5. Для электрической цепи, приведенной в примере 1, определить комплексную передаточную проводимость характеристики, используя операторную характеристику. Решение. Найдем операторную характеристику цепи (рис.40).
Рис. 40
Подставив в последнее выражение значение R, L, C, получим
Комплексная передаточная проводимость
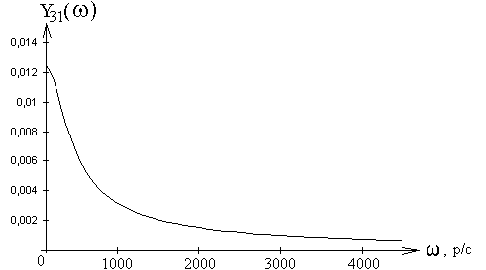
Амплитудно-частотная характеристика
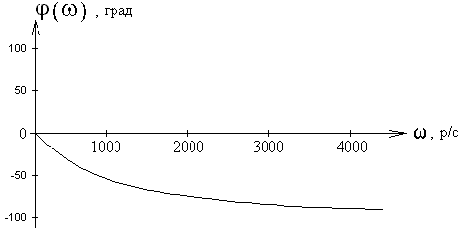
Фазочастотная характеристика
Графики амплитудно-частотной и фазочастотной характеристик приведены на рис.41, 42.
Рис. 41
Рис. 42
|


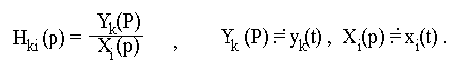




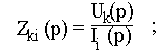
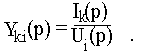

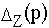 - определитель системы уравнений, составленных методом контурных токов (в операторной форме),
- определитель системы уравнений, составленных методом контурных токов (в операторной форме),
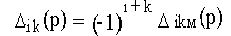 .
.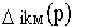 равен определителю системы, из которого исключена i-я строка, соответствующая i-ому контуру, где действует ЭДС Еi(p), и k-й столбец, соответствующий искомому k-ому току.
равен определителю системы, из которого исключена i-я строка, соответствующая i-ому контуру, где действует ЭДС Еi(p), и k-й столбец, соответствующий искомому k-ому току.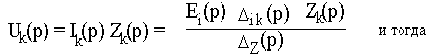
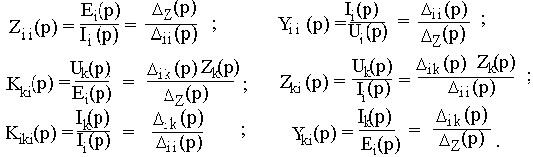
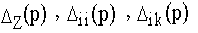

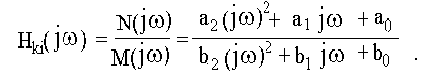
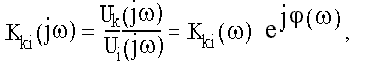
 - амплитудно-частотная характеристика (АЧХ), а
- амплитудно-частотная характеристика (АЧХ), а
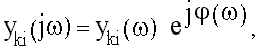 где - АЧХ, j(w) - ФЧХ.
где - АЧХ, j(w) - ФЧХ.