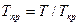Коэффициент сверхсжимаемости природных газов
Как известно, соотношение между параметрами – характеристиками состояния газа (давлением, объемом и температурой) - определяется законами газового состояния. Для идеального газа это уравнение Клапейрона - Менделеева:
где m - масса газа; М – его молярная масса, R – универсальная газовая постоянная, T – абсолютная температура, Р - давление, V – объем газа. Но реальные газы не подчиняются этому закону. Для математического описания состояния реальных газов выявились два пути: 1. Первый путь Введение поправочных членов в уравнение Клапейрона - Менделеева: * Уравнение Ван-дер-Ваальса, в котором введены две константы, учитывающие взаимодействие молекул газа и их собственный объем:
где V – объем газа; Последнее уравнение записано для одного моля вещества. Для вещества, имеющего массу m, уравнение запишется в виде:
* Уравнение состояния Редлиха-Квонга, в котором
* Уравнение Пенга-Робинсона, включающее 3 константы:
Третья константа s в этом уравнении учитывает нецентральность сил взаимодействия между сложными молекулами. Кроме этих уравнений известны также уравнения Битти-Бриджмена с 5 константами и уравнение Бенедикта-Вебба-Рубина, в которое введены 8 констант и другие (как известно, в физике существует множество модификаций уравнения Ван-дер-Ваальса: уравнения Диттеричи, Бертло, Клаузиуса, Камерлинга-Оннеса и т.д.).
2. Второй путь – введение в уравнение коэффициента, характеризующего степень отклонения реального газа от закона идеального газа – коэффициента сверхсжимаемости газа Z:
Характер изменения функции
В идеальных газах (по определению «силами взаимодействия между молекулами можно пренебречь») молекулы занимают незначительный объем по сравнению с объемом газа и не испытывают сил притяжения друг к другу. В реальных газах молекулы обладают определенными размерами и массой и взаимодействуют друг с другом (поэтому реальный газ приближается к идеальному при низких давлениях, когда число молекул в единице объема мало и Z=1). Далее рассмотрение процесса можно разделить на следующие этапы: А). С повышением давления молекулы сближаются и вначале притягиваются, помогая внешним силам сжимать газ, т.е. реальные газы сжимаются сильнее, а Z уменьшается. Б). Затем, когда газ сжат до такой степени, что близок по свойствам к жидкости, начинают действовать силы отталкивания и степень сжатия меньше, чем при малых давлениях, т.е. Z возрастает при дальнейшем увеличении Р.
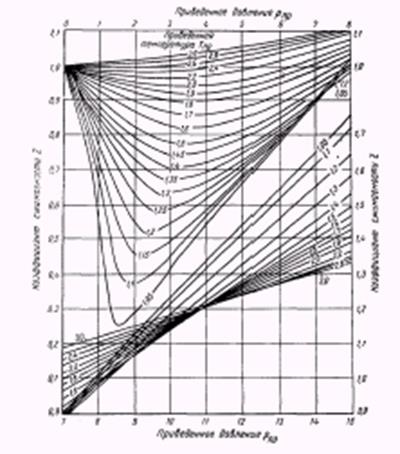
Рис.2.1.3. Зависимость коэффициента сверхсжимаемости природного газа от приведенных абсолютных давления Рпр и температуры Тпр.
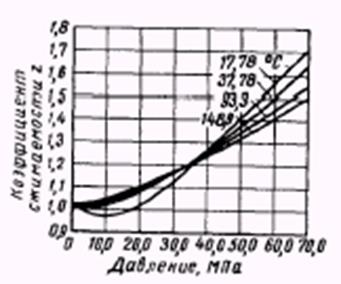
Рис.2.1.4. Зависимость коэффициента сверхсжимаемости азота от давления и температуры.
Вопросы для закрепления: 1. В каких фазовых состояниях могут находиться флюиды в земной коре? 2. На какие основные виды подразделяют продуктивные залежи в зависимости от фазового состояния и соотношения углеводородов? 3. Какие залежи относят к газоконденсатным и газогидратным? 4. Как классифицируют нефти по групповому составу? 5. В чем особенность физических свойств АСВ нефти? 6. Как зависят плотность и вязкость нефти от давления и температуры? 7. Как зависят плотность и вязкость газа от давления и температуры? 8. В чем состоят законы Дальтона и Амага для газов? 9. Как рассчитывают плотность смеси газов? 10. Что такое коэффициент сверхсжимаемости газов? Поясните его зависимость от давления и температуры.
|

 ,
, ,
,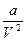 - слагаемое, учитывающая силу притяжения молекул газа, b – поправка на собственный объем молекул (а =3pкрV2кр; b =Vкр /3; pкр, Vкр – критические параметры).
- слагаемое, учитывающая силу притяжения молекул газа, b – поправка на собственный объем молекул (а =3pкрV2кр; b =Vкр /3; pкр, Vкр – критические параметры).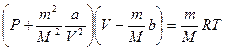
 , т.е.
, т.е.

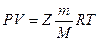 , где
, где 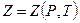
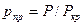 ,
,