|
Правило
| Примеры
|
| –x(x+7)=(x–2)(x+2)
| х2−6х+9=0
|
1. Определить, явл. ли уравнение уравнением вида  . Если «да», то п. 4, если «нет», то п. 2.
| нет
| да
|
| 2. Если нужно, раскрыть скобки; привести к общему знаменателю; поделить на число, не равное нулю; привести подобные слагаемые.
| Раскрыть скобки, используя формулу разности квадратов.
–x2–7x=x2–4
|
___________
|
| 3.Перенести все члены получившегося уравнения в левую часть уравнения меняя при этом знак на противоположный. Привести подобные слагаемые. Т.е. привести уравнение к виду .
| –x2–7x– x2+4=0
–2x2–7x+4=0
|
__________
|
| 4. Выписать коэффициенты уравнения (a, b, c).
| a= –2 b= –7 c=4
| a=1, b= −6, c=9
|
| 5. Вычислить дискриминант по формуле: D=b2-4ac
| D= b2−4ac=(−7)2−4.(−2).4= =49+32=81
| D=b2−4ac=
=(−6)2−4.1.9=
=36−36=0
|
6. Если D<0, то решений нет
Если D=0, то 
Если D>0, то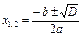 
| D>0Þ 2 решения
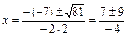
Ответ: x=-4; 0,5
| D=0Þ
Один корень
Ответ: х=3
|
Коррекционная карточка 8 класс:
