Решение. 1. Начертим схему согласно исходным данным.1. Начертим схему согласно исходным данным.
2. Составим 3 уравнения по I закону Кирхгофа:
Составляем контурные уравнения по II закону Кирхгофа: (в-вит)-(y-1)=(7-1)-(4-1)=6-3=3 (уравнения):
Решая, систему получим: I14= -0,012 A I21= -0,655 A I23= -0,845 A I31= 0,643 A I43= 1,488 A E24= 137,333 B
3. Определим неизвестные токи, применив метод контурных токов: Составляем систему уравнений:
Контурные ЭДС: E11=Eэ- E21-E14 Rэ=40 Ом E11= E24-24 B E22= 110 B E33= -70 B
Контурные токи: I24= 0, 6 A
Собственные сопротивления контуров: R11=RЭ+R14+R12=40+80+80=200 Ом R22=R14+R34+R31=80+40+80=200 Ом R33=R12+R31+R23=80+80+40=200 Ом R12=R21=-R14=-80 Ом R13=R31=-R14=-80 Ом R23=R32=R31=-80 Ом
Подставим значения в систему:
Решая, систему получаем:
E43= 137,333 B Определим неизвестные токи: I14= I22- I11= -0,012 A I21= I33-I11=-0,655 A I31= I22-I33 = 0,643 A I43= I22 = 1,488 A I23=-0,845 A E24= 137,333 B
4. Составим уравнение баланса мощности:
I24 =
199,1=199,1
5. Рассчитаем j1, j2, j3 методом узловых потенциалов: Заземляем 4 узел, т.е. j4=0.
Решая, систему уравнений получим:
φ1= -56,657 В φ2= -113,314 В φ3= -16,657 В
Используя метод эквивалентных преобразований резистивных элементов
Определяем входное сопротивление Rвх:
Определяем ток в элементе R12, применив метод эквивалентного генератора.
ЗАДАНИЕ №2 “Применение символических изображений при расчете установившегося процесса цепи с источником синусоидальных ЭДС”.
|
A
А
см
см
см
см
см
см
см
см
см
A
А
А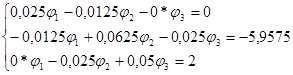
Ом
Ом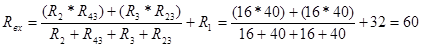
Ом
Ом
В
A
