Необхідність, місце та роль аудиту в системі управління.

Дата добавления: 2015-08-17; просмотров: 606

Предположим, что точки (х_i у_i ) группируются около не­которой прямой.

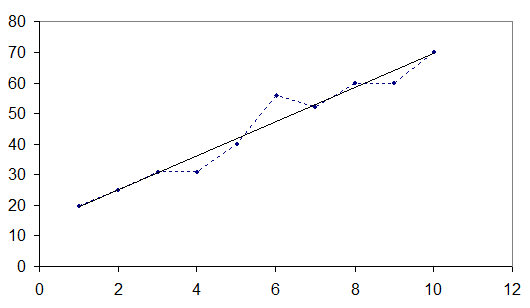
рис 1.

В этом случае между переменными X и У существует функциональная зависимость, близкая к линейной. Будем искать эту зависимость в виде:

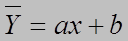(1.1)

где a и b – параметры, подлежащие, вычислению,

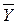- теоретическое значение функции (вычисленное по формуле).

Поставим задачу: найти такие значения а и b, чтобы прямая (1.1.) «наилучшим образом» проходила через множество точек М_i (x_i, y_i).

Если бы все точки M_i(x_i, y_i ) лежали строго на пря­мой (1.1), то для каждой из точек было бы справедливо следую­щее равенство:

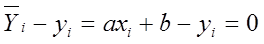
однако на практике имеет место следующее равенство:

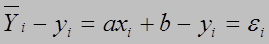(1.2)

т.е существует 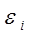(отклонение) между наблюдаемыми ординатами (эмпирическими) и ординатами, полученными по урав­нению (теоретическими).

Принцип метода наименьших квадратов утверждает: оптимальны такие значения параметров а и b при которых сумма квадратов отклонений минимальна. Составим эту сумму:

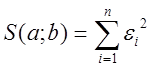или

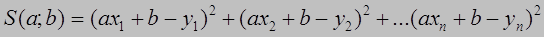(1.3)

Для исследования функции (1.3) с двумя переменными на ми­нимум, найдем частные производные, приравняем их к нулю и решив систему уравнений, найдем а и b.

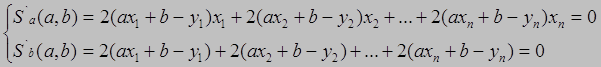(1.4)

или

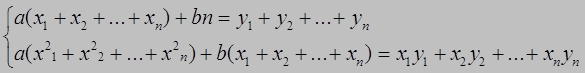(1 .5)

Введя сокращенные обозначения, получим систему уравнений (1.5) в следующем виде:

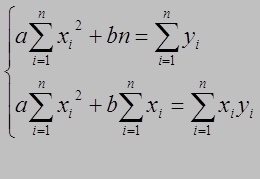(1.6 )

Решив систему (1.6), найдем значения параметров а и b и подставим их значения в эмпирическую формулу (1.1).

Нахождение линейной функциональной зависимости называется выравнивание по прямой, а система уравнений (1.6) - нормальной системой метода наименьших квадратов при выравнивании по прямой.