Класифікація видів аудиту

Дата добавления: 2015-08-17; просмотров: 491

1. Для определения вида функциональной зависимости построим в прямоугольной системе координат точки с координатами:

(1;1,7); (2,1,4); (3,1,5); (4;1,5); (5,1,6); .(6,1,6); (7;1,65); (8;1,66); (9;1,7).

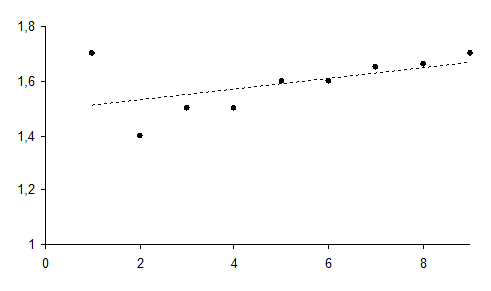
рис 3.

Точки группируются около некоторой линии. Следовательно зависимость между переменными Х и У близка к линейной

2.Для вычисления параметров a и b воспользуемся расчетной таблицей № 3.

Таблица № 3.

х у х2 ху 1,7 1,7 1,4 2,8 1,5 4,5 1,5 1,6 1,6 9,6 1,65 11,55 1,66 13,28 1,7 15,3 14,31 285 72,73

3. Напишем нормальную систему уравнений метода наименьших квадратов (См 1.6).

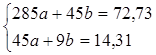(3.1)

4. Решим систему по правилу Крамера, вычислим параметры a, b с точностью до 0,1.

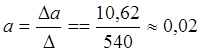
5.Подставляя найденные значения параметров в формулу ,получим эмпирическую формулу:

(3.2)

выражающую зависимость между начисленной месячной пенсии и месяца года.

6. Используя формулу (3.2), можем найти теоретические значения У для данных значений Х и откло­нение теоретической ординаты от эмпирической:

при х= 1 у=0,02*1+1,5=1,52; ε₁=1,52-1,7= -0,18

при х=2 у=0,02*2+1,5=1,54; ε₂=1,54-1,4 = 0,14

при х=3 у=0,02*3+1,5=1,56; ε₃=1,56-1,5 = 0,06

при х=4 у=0,02*4+1,5=1,58; ε₄=1,58-1,5= 0,08

при х=5 у=0,02*5+1,5=1,6; ε₅=1,6-1,6 = 0

при х=6 у=0,02*6+1,5=1,62; ε₆=1,62-1,6= 0,02

при х=7 у=0,02*7+1,5=1,64; ε₇=1,64-1,65= -0,01

при х=8 у=0,02*8+1,5=1,66; ε₈=1,66-1,66=0

при х=9 у=0,02*9+1,5=1,68; ε₉=1,68-1,7= -0,02.

Сумма отклонений ε_i должна быть близкой к 0.

С помощью формулы можно найти значения У для тех значений X, которое не содер­жатся в таблице, но взяты из области изменения X (интерполировать). Этот факт и оправдывает отыскание эмпирических формул.

Например, пусть Х=4,5, тогда У=0,02*4,5+1,5=1,59.

Отсюда, у_х=4,5 = 1,59 т.е. в середине апреля, будет назначена месячная пенсия в размере 1,59 тыс.руб.

Можно найти значение функции для значения X, выходящего за пределы таблицы, (экстраполировать),т.е. находить прогнозную оценку.

Например, при х=10, У=0,02*10+1,5=1,7, т.е. в октябре будет назначена месячная пенсия в размере 1,7 тыс.руб.

7. Выясним содержательный смысл параметров полученного уравне­ния =0,02х+1,5.

Коэффициент, а =0,02 определяет средний показатель уве­личения месячной пенсии. С каждым месяцем начисленная месячная пенсия увеличивается в среднем на 0,02 тыс.руб.

Свободный член b=1,5 конкретного содержательного смысла не имеет, он определяет начальный уровень.

6.Наглядно убедимся в том, насколько хорошо теоретическая кривая согласуется с исходными данными. Для этого построим точки с координатами: (1;1,7); (2,1,4); (3,1,5); (4;1,5); (5,1,6); .(6,1,6); (7;1,65); (8;1,66); (9;1,7) и полученную теоретическую прямую по точкам (0;1,5); (2;1,54) (рис.4).

На рисунке видно, что погрешности (отклонения ε_i ) теоретических ординат от эмпирических малы по абсолютной величине. Следовательно, теоретическая функция хорошо согласуется с исход­ными данными.

Рис. 4