Користувачі аудиту та їх цілі

Дата добавления: 2015-08-17; просмотров: 696

Пусть точки М_i(x_i, y_i), соответствующее парам чисел таблицы 1, группируются вблизи некоторой параболы (рис 2).

рис 2.

В этом случае между переменными Х и У существует функциональная зависимость, которую будем искать в виде:

(1.7)

Найдем параметры a, b и c с таким расчетом, чтобы парабола заданная уравнением (1.7) «наилучшим образом» проходила через множество точек М_i(x_i, y_i), т.е чтобы сумма квадратов отклонений теоретических ординат точек от эмпирических была наименьшей.

Составим эту сумму:

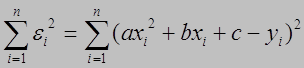(1.8)

Найдем частные производные по переменным a, b, и c, при­равняем их к нулю, преобразуем полученные уравнения и получим следующую систему уравнений:

(1.9)

Система уравнений (1.9) называется нормальной системой ме­тода наименьших квадратов при выравнивании по параболе.

Решив систему уравнений, найдем параметры a, b, c и подставим их значения в уравнение (1.7). Получим искомую эмпирическую функцию.

Замечание I. Число уравнений нормальной системы уравнений (1.6) и (I..9) метода наименьших квадратов соответствует числу ис­комых параметров.

Замечание 2. Между переменными х и у , заданными табли­цей, существуют зависимости, близкие, например, к показательной функции вида у= аb^x или lgy, lga+xlgb; к функции y=a/x+b (уравнение гиперболы) и др.