Способи задання функції

Дата добавления: 2015-08-17; просмотров: 728

2.1. Определение вращающего момента асинхронной машины на основании закона электромагнитных сил

Возникновение электромагнитных сил и вращающих моментов в асинхронной машине является результатом взаимодействия распреде­ленных вдоль окружности ротора гармоник тока и индукции магнитно­го поля того же порядка. (Гармоники разных порядков создают вдоль окружности ротора знакопеременные электромагнитные силы и момен­ты, суммарная величина которых равна нулю).

На рис.6 показана кривая индукции основной гармоники резуль­тирующего магнитного поля в зазоре асинхронной машины

B=B_msin(πx/τ), (45)

При вращении этого поля в каждом проводнике обмотки ротора наво­дится переменная ЭДС, мгновенное значение которой равно e₂=Bl_δv. Эта ЭДС так же, как и магнитная индукция, распределяет­ся вдоль окружности ротора по синусоидальному закону

(46)

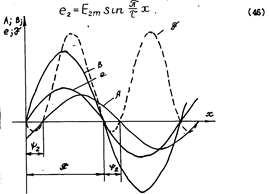
Рис.6. Кривые распределения индукции В, ЭДС е, линейной плотности тока А, электромагнитных сил в асинхронной машине.

Направление этих ЭДС определяется по правилу правой руки. Под действием ЭДС е₂ в каждом проводнике обмотки ротора протекает ток i₂, линейная плотность которого А₂ (сумма токов на единицу длины окружности) связана с МДС F₂ выражением А₂=F₂. Она распределяется вдоль окружности ротора по синусоидальному закону для любого момента времени. Ток i₂ отстает от ЭДС на угол ψ₂. Тогда

A₂=A_m2sin(πx/τ-ψ₂), (47)

Взаимодействие плотности тока А₂ с бегущим вдоль окружности рото­ра магнитным полем В приводит к появлению электромагнитных сил F, которые действуют на проводники c током

F=Bl_δA₂, (48)

Элементарный момент развиваемый электромагнитными силами, дейст­вующими на протяжении элемента длины окружности ротора dx, ра­вен,

где Da=2pτ/π - диаметр ротора.

В полученную формулу для элементарного момента подставим выраже­ния для плотности А₂ (47) и магнитной индукции В (45) и, выпол­нив преобразования, получим

Зависимость d(M)=f(x) изображена на риc.6. Легко отметить, что к проводникам, лежащим на дуге, соответствующей углу (π-ψ₂) приложены моменты, увлекающие ротор за вращающимся магнитным по­током, а на дуге, соответствующей углу ψ₂ - тормозящие момен­ты.

где x_K=x₁+x₂’;

знак (+) соответствует работе асинхронной машины в качестве двигателя, знак (-) - в качестве генератора. Подставляя положительное значение S_K (57) в выражение для электромагнитного момента (56), получим выражение для критичес­кого момента в двигательном режиме

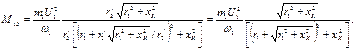Раскроем круглые скобки в знаменателе полученного выражения и разделим числитель и знаменатель на получим

(58)

Подставляя отрицательное значение S_K (57) в выражение для электромагнитного момента (56),

получим аналогичное выражение для критического момента асинхронной машины в генераторном режи­ме

(59)

Найдем отношение критических моментов асинхронной машины в гене­раторном и двигательном режимах

(60)

где (61)

Таким образом, значение критического момента в генераторном ре­жиме больше, чем в двигательном, что обусловлено влиянием паде­ния напряжения на активном сопротивлении обмотки статора.

В практических расчетах удобно выражать электромагнитный момент M в долях от максимального момента M_кд

В полученном выражении числитель и знаменатель разделим на

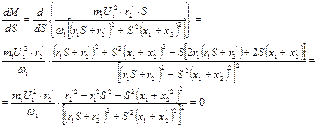Анализ полученного выражения показывает, что оно обратится в нуль, если

r ^/2₂ – r ²₁ S² - S² (x₁ + x ^/₂)² = 0

Рис.9. Механические характеристики асинхронной машины а - зависимость M=f(S), б - зависимость S=f(M)

или r ^/2₂ = S² [r ²₁ + (x₁ + x ^/₂)²].

Тогда критическое скольжение S_K, при котором момент асинхронной машины имеет максимальное значение, равно

(57)

Результирующий электромагнитный момент найдем путем интегрирования элементарного по x

Принимая во внимание, что

Окончательно получим

M= 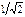pm₂w₂k_об2Ф_mI₂cosψ₂=C_MФ_mI₂cosψ₂, (49)

где C_M= pw₂k_об2 - постоянный коэффициент.

Таким образом, при неизменных токе I₂ и магнитном поле величина результирующего электромагнитного момента M тем меньше, чем больше угол ψ₂. При ψ₂=π/2 момент M=0, так как на половину проводников действует усилие, направленное в од­ну сторону, а на другую половину - такое же усилие, направленное в другую сторону. Формула (49) позволяет связать величину момен­та с физическими явлениями, происходящими в двигателе, и ею удоб­но пользоваться для качественного анализа поведения асинхронной машины в различных режимах.