РОЗДІЛ І. ТЕОРЕТИКО-МЕТОДОЛОГІЧНІ ОСНОВИ ДОСЛІДЖЕННЯ КРАЇН ЄВРОПЕЙСЬКОГО СОЮЗУ

Дата добавления: 2015-08-30; просмотров: 563

Характеристики движения жидкости. Гидродинамика, изучая закономер­ности движения, решает три задачи: внутреннюю, внешнюю и смешанную.

Внутренняя задача связана с анализом движения жидкостей внутри труб и каналов.

Внешняя задача изучает закономерности обтекания жидкостями различ­ных тел (при механическом перемешивании, осаждении твердых частиц в жидкости и т. п.).

Смешанная задача решается при движении жидкости через зернистый слой твердого материала, когда она перемещается как внутри каналов слож­ной формы, так и одновременно обтекает твердые частицы. Такие условия наблюдаются в процессах фильтрования, массопередачи в аппаратах с на­садками, сушки и т. д. Анализ движения жидкостей в случаях такой сме­шанной задачи гидродинамики проводят приближенно, сводя его к реше­нию внутренней или внешней задачи.

Движущей силой при течении жидкостей является разность давлений, которая создается с помощью насосов или компрессоров, либо вследствие разности уровней или плотностей жидкости.

Знание законов гидродинамики позволяет находить разность давлений, необходимую для перемещения данного количества жидкости с требуемой скоростью, а значит, и расход энергии на это перемещение, или наоборот — определять скорость и расход жидкости при известном перепаде давления.

Классификация видов движения жидкости.Классификация осущест­вляется по нескольким признакам.

1. По зависимости скорости от координат и времени движения делятся на установившиеся и неустановившиеся (стационарные и нестационарные).

Неустановившееся движение — это такое движение, когда параметры движущейся жидкости в различных точках занимаемого ею пространства изменяются с течением времени. Для такого движения скорость, например, может быть функцией всех трех координат и обязательно зависит от време­ни и = и(х, у, z, τ). Подчеркнем, что для неустановившегося движения зави­симость параметров от всех трех координат не обязательна. Они могут изме­няться вдоль двух или даже одной координаты. Обязательной же является зависимость от времени. Движения жидкости, характеризующееся соотно­шениями и = и(х, у, τ) и и = и(х, τ), также являются неустановившимися.

Примером неустановившегося движения может служить течение жид­кости в трубе, соединяющей бак с атмосферой, при естественном опорожне­нии бака. С течением времени скорость жидкости будет уменьшаться, а ког­да вся жидкость вытечет, движение вообще прекратится.

Установившееся движение — это такое движение, когда параметры дви­жущейся жидкости в различных точках пространства с течением времени не изменяются. Для такого движения скорость, например, является функ­цией только координат и не зависит от времени и = и(х, у, z).

Примером установившегося движения может служить также течение жидкости в трубе, соединяющей бак с атмосферой, но в том случае, когда в бак подводится жидкость в количестве, равном количеству жидкости, выте­кающей из трубы в атмосферу.

Установившееся движение может быть равномерным и неравномерным.

Равномерным движением называется такое, при котором скорости частиц жидкости в сходственных точках двух смежных сечений равны между собой (и = idem). Неравномерным — при котором скорости частиц жидкости в сходственных точках двух смежных сечений не равны между собой (и = var). Неравномерное движение в зависимости от характера изменения сечения тру­бопровода делится на плавноизменяющееся и резкоизменяющееся.

Примером равномерного движения является течение жидкости с постоян­ным расходом в прямой трубе постоянного диаметра на участке, расположен­ном достаточно далеко от входа в трубу. Если сечение трубопровода по длине бу­дет изменяться, то движение в нем будет установившимся неравномерным.

2. По наличию вращательного движения частиц жидкости движения де­лятся на безвихревые (вращение отсутствует) — потенциальные и вихревые.

Среди вихревых движений имеет место частный случай — винтовое движе­ние, при котором вектор угловой скорости совпадает с направлением вектора линейной скорости в данной точке. Движение жидкой частицы отличается от движения абсолютно твердой частицы. Твердая частица может двигаться или поступательно (хотя бы и непрямолинейно), или вращательно, или поступа­тельно с вращением, но ее форма при этом сохраняется неизменной.

Жидкая частица, сохраняя свой объем (если жидкость несжимаемая), может в своем движении, кроме того, и деформироваться. В общем случае она осуществляет все три вида движения, потому движение жидкой части­цы можно разложить на поступательное, вращательное и деформационное — теорема Коши — Гельмгольца.

В частном случае, если в пространстве, в котором находится данная час­тица, скорости во всех точках равны между собой и параллельны друг другу, ее движение поступательное.

3. По наличию свободной поверхности движения делятся на напорные, безнапорные и свободные.

Напорным называется движение жидкости, не имеющей свободной поверх­ности. Примером такого движения может служить движение жидкости в тру­бопроводе при полном заполнении его сечения, например воды в водопроводе.

Безнапорным движением называется движение жидкости со свободной по­верхностью в открытых и закрытых руслах (рис.4.1). Примером такого движе­ния может служить движение воды в реках, бытовых стоков в канализационных коллекторах. Безнапорное движение может быть разделено на спокойное, бурное и критическое в зависимости от критической глубины потока h .

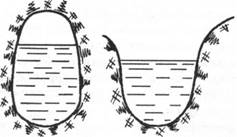
Рис. 4.1. Безнапорное течение жидкости

Для спокойного движения (течение воды в равнинных реках) глубина по­тока h > h_кр; для бурного движения (течение воды в горных реках) h < h_кр; для критического движения h = h_кр.

Свободным является движение жидкости, нигде не стесняемое твердыми стенками русла. Свободное движение жидкости называется струями. Струи могут быть затопленные и незатопленные.

Затопленной струей называется такое движение, при котором плотность движущейся жидкости примерно равна плотности окружающей среды. Напри­мер, затопленной является струя дыма, выходящая из трубы, струя промывочного раствора, бьющая из сопла гидромониторного долота. Незатопленной струей называется такое движение, при котором плотность движущейся жид­кости намного превышает плотность окружающей среды. Это, например, фон­танная струя или струя воды из пожарного брандспойта.

4. Движение может быть сплошным и прерывистым. Сплошным, или не­прерывным движением, называется такое движение, при котором жидкость сплошь заполняет всю область своего движения. Прерывистым является движение жидкости при наличии пустот в области движения. Обычное тече­ние в реках — сплошное, а на водопадах — прерывистое.

5. Движение может быть осесимметричным (поле скоростей и ускорений име­ет одинаковый вид в любых плоскостях, проходящих через некоторую прямую, называемую осью симметрии) и неосесимметричным. Примером осесимметричного движения может служить движение жидкости в круглых трубках.

6. Движения можно разделить на одномерные, двухмерные (плоскопа­раллельные) и трехмерные.

Трехмерное движение — это такое движение, когда параметры потока из­меняются вдоль всех трех координат (рис.4.2). Трехмерное движение мо­жет быть как неустановившимся, так и установившимся.

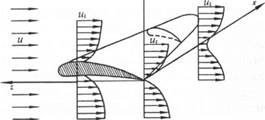
Рис. 4.2. Трехмерное движение при обтекании крыла

Примером трехмерного движения в прямоугольной системе координат мо­жет служить обтекание потоком любого тела конечных размеров, например, крыла. Если проследить, как изменяется скорость потока вдоль каждой из трех координат, то видно, что при фиксированном значении двух любых ко­ординат (например, у = z = 0) скорость изменяется вдоль третьей координаты. Напомним, что изменение скорости вблизи твердой поверхности обусловлено «прилипанием» частичек жидкости к этой поверхности.

Двухмерное движение — это такое движение, когда параметры потока изменяются только вдоль двух координат. Оно также может быть неустано­вившимся и установившимся.

Примером двухмерного движения в прямоугольной системе координат может служить обтекание потоком бесконечного цилиндра (рис.4.3.). Не­трудно заметить, что в отличие от предыдущего случая здесь происходит из­менение скоростей только вдоль осей у и z. Вдоль оси х скорость не изменя­ется при любых фиксированных значениях у и z.

Рис. 4.3. Двухмерное движение при обтекании бесконечного цилиндра

Двухмерное движение всегда является плоскопараллельным, удовлетво­ряющим двум условиям:

а) в данный момент времени область движения можно пересечь такими плоскими параллельными поверхностями, в которых лежат векторы скоро­стей и ускорений, отвечающие всем точкам этих поверхностей;

б) во всех точках любого перпендикуляра, проведенного к указанным по­верхностям, скорости и ускорения в данный момент времени одинаковы (по величине и направлению).

Одномерное движение — это такое движение, когда параметры потока изменяются только вдоль одной координаты.

Примером одномерного движения в прямоугольной системе координат мо­жет служить обтекание потоком бесконечной плоской пластины (рис.4.4). В этом случае скорость изменяется только в направлении нормали к поверхнос­ти пластинки, т. е. вдоль координаты у. Одномерное течение также всегда явля­ется плоскопараллельным. Его называют также линейным движением.

Вполне очевидно, что одномерное движение является простейшим для анализа видом движения. При этом следует отметить, что иногда от выбора системы координат зависит, будет ли движение трехмерным, двухмерным или даже одномерным. Например, при движении жидкости в цилиндричес­кой трубе переход от прямоугольной к цилиндрической системе координат переводит задачу из двухмерной в одномерную.

Рис.4.4. Одномерное движение при обтекании бесконечной плоской пластины

7. Движения можно классифицировать по механизму передачи количест­ва движения между слоями жидкости. Если этот механизм имеет молекуляр­ную природу, движение называется ламинарным. Если количество движения передается в основном за счет обмена жидкими массами, перемещающимися хаотически во всем объеме жидкости, движение называется турбулентным. Турбулентное движение можно дополнительно разделить на движение в зо­нах гладкого, смешанного и шероховатого сопротивления (трения).

Для лучшего представления о связи между различными видами движе­ния на рис.4.5 показана классификационная схема движений по Л. С. Абразону, пользуясь которой, можно достаточно полно охарактеризовать любое течение.

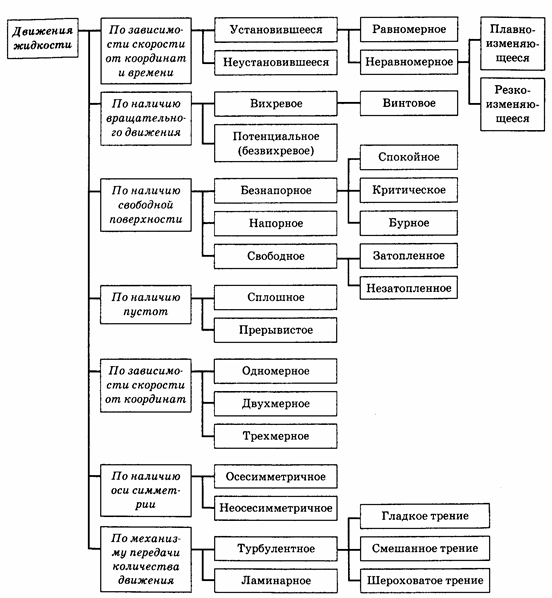
Рис.4.5. Классификация движений жидкости