
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Розвиток промисловості
Дата добавления: 2015-08-30; просмотров: 667
|
|
Назначение критерия
Критерий λпредназначен для сопоставления двух распределений:
- эмпирического с теоретическим, например, равномерным или нормальным;
- одного эмпирического распределения с другими эмпирическим распределением.
Критерий позволяет найти точку, в которой сумма накопленных расхождений между двумя распределениями является наибольшей, и оценить достоверность этого расхождения.
Описание критерия
Если в методе  мы сопоставляли частоты двух распределений отдельно по каждому разряду, то здесь мы сопоставляем сначала частоты по первому разряду, потом по сумме первого и второго разрядов, потом по сумме первого, второго и третьего разрядов и т. д. Таким образом, мы сопоставляем всякий раз накопленные к данному разряду частоты.
мы сопоставляли частоты двух распределений отдельно по каждому разряду, то здесь мы сопоставляем сначала частоты по первому разряду, потом по сумме первого и второго разрядов, потом по сумме первого, второго и третьего разрядов и т. д. Таким образом, мы сопоставляем всякий раз накопленные к данному разряду частоты.
Если различия между двумя распределениями существенны, то в какой-то момент разность накопленных частот достигает критического значения, и мы сможем признать различия статистически достоверными. В формулу критерия λвключается эта разность. Чем больше эмпирическое значение λ, тем более существенны различия.
Гипотезы
H0: Различия между двумя распределениями недостоверны (судя по точке максимального накопленного расхождения между ними).
H1: Различия между двумя распределениями достоверны (судя по точке максимального накопленного расхождения между ними).
Графическое представление критерия
Рассмотрим для иллюстрации распределение желтого (№4) цвета в 8-цветном тесте М. Люшера. Если бы испытуемые случайным образом выбирали цвета, то желтый цвет, так же, как и все остальные, равновероятно мог бы занимать любую из 8-и позиций выбора. На практике, однако, большинство испытуемых помещают этот цвет, «цвет ожидания и надежды» на одну из первых позиций ряда.
На рисунке столбиками представлены относительные частоты попадания желтого цвета сначала на 1-ю позицию (первый левый столбик), затем на 1-ю и 2-ю позицию (второй столбик), затем на 1-ю, 2-ю и3-ю позиции и т. д.
Мы видим, что высота столбиков постоянно возрастает, так как они отражают относительные частоты, накопленные к данной позиции. Например, столбик на 3-й позиции имеет высоту 0,510. Это означает, чтона первые три позиции желтый цвет помещают 51% испытуемых.
Прерывистой линией на рисунке соединены точки, отражающие накопленные частоты, которые наблюдались бы, если бы желтый цвет с равной вероятностью попадал на каждую из 8-и позиций. Сплошными линиями обозначены расхождения между эмпирическими и теоретическими относительными частотами. Эти расхождения обозначаются как d.

Сопоставления в критерии λ: стрелками отмечены расхождения между эмпирическими и теоретическими накопленными относительными частотами по каждому разряду
Максимальное расхождение обозначено как dmax. Именно эта, третья позиция цвета, и является переломной точкой, определяющей, достоверно ли отличается данное эмпирическое распределение от равномерного. Мы проверим это при рассмотрении примера.
Ограничения критерия λ
1. Критерий требует, чтобы выборка была достаточно большой. При сопоставлении двух эмпирических распределений необходимо, чтобы 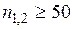 . Сопоставление эмпирического распределения с теоретическим иногда допускается при
. Сопоставление эмпирического распределения с теоретическим иногда допускается при  .
.
2. Разряды должны быть упорядочены по нарастанию или убыванию какого-либо признака. Они обязательно должны отражать какое-то однонаправленное его изменение. Например, мы можем за разряды принять дни недели, 1-й, 2-й, 3-й месяцы после прохождения курса терапии, повышение температуры тела, усиление чувства недостаточности и т. д. В то же время, если мы возьмем разряды, которые случайно оказались выстроенными в данную последовательность, то и накопление частот будет отражать лишь этот элемент случайного соседства разрядов. Например, если шесть стимульных картин в методике Хекхаузена разным испытуемым предъявляются в разном порядке, мы не вправе говорить о накоплении реакций при переходе от картины №1 стандартного набора к картине №2 и т. д. Мы не можем говорить об однонаправленном изменении признака при сопоставлении категорий «очередность рождения», «национальность» ,»специфика полученного образования» и т.п. Эти данные представляют собой номинативные шкалы: в них нет никакого однозначного однонаправленного изменения признака.
Итак, мы не можем накапливать частоты по разрядам, которые отличаются лишь качественно и не представляют собой шкалы порядка. Во всех тех случаях, когда разряды представляют собой не упорядоченные по возрастанию или убыванию какого-либо признака категории, нам следует применять метод  .
.
Алгоритм расчета абсолютной величины разности d между эмпирическим и равномерным распределением
1 Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты (первый столбец).
2 Подсчитать относительные эмпирические частоты (частости) для каждого разряда по формуле: 
где fj - частота попадания желтого цвета на данную позицию;
п – общее количество наблюдений;
j – номер позиции по порядку.
Занести результаты во второй столбец.
3 Подсчитать накопленное эмпирические частости 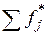 .по формуле:
.по формуле:
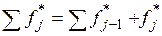 ,
,
где  – частость, накопленная на предыдущих разрядах;
– частость, накопленная на предыдущих разрядах;
 ;– эмпирическая частость данного j-го разряда. Занести результаты в третий столбец таблицы.
;– эмпирическая частость данного j-го разряда. Занести результаты в третий столбец таблицы.
4 Подсчитать накопленные теоретические частости для каждого разряда по формуле:
 где
где  – теоретическая частость, накопленная на предыдущих разрядах;
– теоретическая частость, накопленная на предыдущих разрядах;
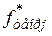 – теоретическая частость данного разряда.
– теоретическая частость данного разряда.
Занести результаты в третий столбец таблицы.
5 Вычислить разности между эмпирическими и теоретическими накопленными частостями по каждому разряду (между значениями 3-го и 4-го столбцов).
6 Записать в пятый столбец абсолютные величины полученных разностей. Обозначить их как d.
7 Определить по пятому столбцу наибольшую абсолютную величину разности – dmax.
8 По таблице приложения определить или рассчитать критические значения dmax для данного количества наблюдений n. Если dmax равно критическому значению d или превышает его, различия между распределениями достоверны.
Пример 1.
Сопоставление эмпирического распределения с теоретическим
В выборке здоровых лиц мужского пола, студентов технических и военно-технических вузов в возрасте от 19-ти до 22 лет, средний возраст 20 лет, проводился тест Люшера в 8-цветном варианте. Установлено, что желтый цвет предпочитается испытуемыми чаще, чем отвергается. Можно ли утверждать, что распределение желтого цвета по 8-и позициям у здоровых испытуемых отличается от равномерного распределения?
Эмпирические частоты попадания желтого цвета на каждую из 8 позиций ( )
)
| Разряды | Позиции желтого цвета | Сумма | |||||||
| Эмпирические частоты |
Сформулируем гипотезы.
Н0: Эмпирическое распределение желтого цвета по восьми позициям не отличается от равномерного распределения.
Н1: Эмпирическое распределение желтого цвета по восьми позициям отличается от равномерного распределения.
Теперь приступим к расчетам, постепенно заполняя результатами таблицу расчета критерия λ.
Занесем в таблицу наименования (номера) разрядов и соответствующие им эмпирические частоты (первый столбец таблицы).
Затем рассчитаем эмпирические частости по формуле: 
Запишем результаты во второй столбец таблицы.
Теперь нам нужно подсчитать накопленные эмпирические частости 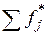 . Для этого будем суммировать эмпирические частости. Например, для 1-го разряда накопленная эмпирическая частость будет равняться эмпирической частости 1-го разряда,
. Для этого будем суммировать эмпирические частости. Например, для 1-го разряда накопленная эмпирическая частость будет равняться эмпирической частости 1-го разряда,  .
.
Для 2-го разряда накопленная эмпирическая частость будет представлять собой сумму эмпирических частостей 1-го и 2-го разрядов:

Для 3-го разряда:  .
.
Запишем результаты этой работы в третий столбец.
Теперь нам необходимо сопоставить накопленные эмпирические частости с накопленными теоретическими частостями. Для 1-го разряда теоретическая частость определяется по формуле:

где k – количество разрядов (в данном случае – позиций цвета)
Длярассматриваемого примера: 
Эта теоретическая частость относится ко всем 8-и разрядам. Действительно, вероятность попадания желтого (или любого другого) цвета на каждую из 8-и позиций при случайном выборе составляет 1/8, т.е. 0,125.
Накопленные теоретические частости для каждого разряда определяем суммированием.
Для 1-го разряда накопленная теоретическая частость равна теоретической частости попадания в разряд: 
Для 2-го разряда накопленная теоретическая частость представляет собой сумму теоретических частостей 1-го и 2-го разрядов:

Для 3-го разряда:  .
.
Занесем рассчитанные накопленные теоретические частости в четвертый столбец таблицы.
Теперь нам осталось вычислить разности между эмпирическими и теоретическими накопленными частостями (столбцы 3-й и 4-й). В пятый столбец записываются абсолютные величины этих разностей, обозначаемые как d.
Расчет критерия при сопоставлении распределения выборов желтого цвета с равномерным распределением (  )
)
| Позиция желтого цвета | Эмпирическая частота | Эмпирическая частость | Накопленная эмпирическая частость | Накопленная теоретическая частость | Разность |
| 0,235 | 0,235 | 0,125 | 0,110 | ||
| 0,147 | 0,382 | 0,250 | 0,132 | ||
| 0,127 | 0,510 | 0,375 | 0,135 | ||
| 0,078 | 0,588 | 0,500 | 0,088 | ||
| 0,147 | 0,735 | 0,625 | 0,110 | ||
| 0,098 | 0,833 | 0,750 | 0,083 | ||
| 0,088 | 0,922 | 0,875 | 0,047 | ||
| 0,078 | 1,000 | 1,000 | 0,000 | ||
| Суммы | 1,000 |
Определим по столбцу 5, какая из абсолютных величин разности является наибольшей. Она будет называться dmax. В данном случае  .
.
Теперь нам нужно обратиться к таблице приложения для определения критических значений dmax при  .
.

Для данного случая:
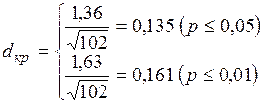
Очевидно, что чем больше различаются распределения, тем больше и различия в накопленных частостях. Поэтому нам не составит труда распределить зоны значимости и незначимости по соответствующей оси:


Ответ: Н0 отвергается при  . Распределение желтого цвета по восьми позициям отличается от равномерного распределения.
. Распределение желтого цвета по восьми позициям отличается от равномерного распределения.
Пример 2. Сопоставление двух эмпирических распределений
Интересно сопоставить данные, полученные в предыдущем примере, с данными обследования X. Кларом 800 испытуемых. X. Кларом было показано, что желтый цвет является единственным цветом, распределение которого по 8 позициям не отличается от равномерного. Полученные им эмпирические частоты представлены в таблице.
Эмпирические частоты попадания желтого цвета на каждую из 8 позиций в исследовании X. Клара
| Разряды – позиции желтого цвета | Сумма | ||||||||
| Эмпирические частоты |
Сформулируем гипотезы.
Н0: Эмпирические распределения желтого цвета по 8 позициям в отечественной выборке и выборке X. Клара не различаются.
Н1: Эмпирические распределения желтого цвета по 8 позициям в отечественной выборке и выборке X. Клара отличаются друг от друга.
Поскольку в данном случае мы будем сопоставлять накопленные эмпирические частости по каждому разряду, теоретические частости нас не интересуют.
Все расчеты будем проводить в таблице по следующему алгоритму.
Алгоритм расчета критерия λ при сопоставлении двух эмпирических распределений
- Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты, полученные в распределении 1 (первый столбец) и в распределении 2 (второй столбец).
- Подсчитать эмпирические частости по каждому разряду для распределения 1 по формуле:

где  – эмпирическая частота в данном разряде;
– эмпирическая частота в данном разряде;
 – количество наблюдений в выборке.
– количество наблюдений в выборке.
Занести эмпирические частости распределения 1 в третий столбец.
- Подсчитать эмпирические частости по каждому разряду для распределения 2 по формуле:

где  – эмпирическая частота в данном разряде;
– эмпирическая частота в данном разряде;
 – количество наблюдений во 2-й выборке.
– количество наблюдений во 2-й выборке.
Занести эмпирические частости распределения 2 в четвертый столбец таблицы.
- Подсчитать накопленные эмпирические частости для распределения 1 по формуле:
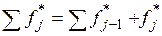 ,
,
где  – частость, накопленная на предыдущих разрядах;
– частость, накопленная на предыдущих разрядах;
 ;– эмпирическая частость данного j-го разряда.
;– эмпирическая частость данного j-го разряда.
Полученные результаты записать в пятый столбец.
- Подсчитать накопленные эмпирические частости для распределения 2 по той же формуле и записать результат в шестой столбец.
- Подсчитать разности между накопленными частостями по каждому разряду. Записать в седьмой столбец абсолютные величины разностей. Обозначить их как d.
- Определить по седьмому столбцу наибольшую абсолютную величину разности dmax.
- Подсчитать значение критерия λ по формуле:

где  –количество наблюдений в первой выборке;
–количество наблюдений в первой выборке;  – количество наблюдений во второй выборке.
– количество наблюдений во второй выборке.
- По таблице приложения определить, какому уровню статистической значимости соответствует полученное значение λ.
Если  , различия между распределениями достоверны.
, различия между распределениями достоверны.
Последовательность выборок может быть выбрана произвольно, так как расхождения между ними оцениваются по абсолютной величине разностей. В нашем случае первой будем считать отечественную выборку, второй – выборку Клара.
Расчет критерия при сопоставлении эмпирических распределений желтого цвета в отечественной выборке (  ) и выборке Клара (
) и выборке Клара (  )
)
| Позиция желтого цвета | Эмпирические частоты | Эмпирические частости | Накопленные эмпирические частости | Разность 
| |||
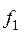
| 
| 
| 
| 
| 
| ||
| 0,235 | 0,123 | 0,235 | 0,123 | 0,113 | |||
| 0,147 | 0,141 | 0,382 | 0,264 | 0,119 | |||
| 0,127 | 0,145 | 0,510 | 0,409 | 0,101 | |||
| 0,078 | 0,109 | 0,588 | 0,518 | 0,071 | |||
| 0,147 | 0,114 | 0,735 | 0,631 | 0,104 | |||
| 0,098 | 0,140 | 0,833 | 0,771 | 0,062 | |||
| 0,088 | 0,121 | 0,922 | 0,893 | 0,029 | |||
| 0,078 | 0,108 | 1,000 | 1,000 | 0,000 | |||
| Суммы | 1,000 | 1,000 |
Максимальная разность между накопленными эмпирическими частостями составляет 0,118 и падает на второй разряд.
В соответствии с пунктом 8 алгоритма подсчитаем значение λ:

По таблице Приложения определяем уровень значимости полученного значения: 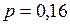
Построим для наглядности ось значимости.

На оси указаны критические значения λ, соответствующие принятым уровням значимости:  ,
,  .
.
Зона значимости простирается вправо, от 1,63 и далее, незначимости – влево, от 1,36 к меньшим значениям.

Ответ: Н0 принимается. Эмпирические распределения желтого цвета по 8 позициям в отечественной выборке и выборке X. Клара совпадают. Таким образом, распределения желтого цвета в двух выборках не различаются, но в то же время они по-разному соотносятся с равномерным распределением: у Клара отличий от равномерного распределения не обнаружено, а в отечественной выборке различия обнаружены ( ). Возможно, картину могло бы прояснить применение другого метода?
). Возможно, картину могло бы прояснить применение другого метода?
Е.В. Гублер предложил сочетать использование критерия λ с критерием φ* (угловое преобразование Фишера).
ЛИТЕРАТУРА
1. ГришвлевЛ.Л- Формирование японской национальной культуры. М., 1986.
2. Кирквуд К. Ренессанс в Японии. М., 1988.
3. Конрад П.И. Очерк истории культуры средневековой Японии. М., 1980.
4. Кузнецов Ю.Л., Навлицкая Г.Б., Сырицын И.М. История Японии. М., 1988.
5. Литературный гид: Культура и литература современной Японии // Иностранная литература. 1993. №5.
6. Преображенский К. Как стать японцем. М., 1989.
ЛЕКЦИЯ
АМЕРИКАНСКАЯ И ЯПОНСКАЯ ШКОЛЫ МЕНЕДЖМЕНТА
Сегодня Америка и Япония являются одними из самых развитых в экономическом плане государств. Именно поэтому развивающиеся страны пытаются эффективно использовать их опыт руководства предприятиями.
В американской школе менеджмента принято считать, что успех фирмы зависит, прежде всего, от внутренних факторов. Особое внимание уделяется рациональной организации производства, постоянному росту производительности труда, эффективному использованию ресурсов, в то время как внешние факторы отходят на второй план. Рационализация производства выражается в высокой степени специализации отдельных работников и структурных единиц компании и жестком разграничении их обязанностей. Преимущества специализации заключаются в том, что она позволяет сократить объем подготовки работников, повысить уровень профессионального умения на каждом специализированном рабочем месте, отделить от производственных заданий те, которые не требуют квалифицированного труда и могут быть выполнены неквалифицированными работниками, получающими меньшую зарплату, а также увеличивает возможности специализированного оборудования.
Решения чаще всего принимаются индивидуально, уровень ответственности в управленческой пирамиде высок, это означает, что руководство отвечает за деятельность своих подчиненных.
Американская фирма функционирует в социальной атмосфере, проповедующей равноправие. Соответственно рабочие здесь являются более мобильными, легко меняют место работы в поисках индивидуальной выгоды. Нужно отметить, что дух «жертвенности» (альтруизма) очень редок у американцев: даже в действиях, направленных на пользу общества, на поверку легко обнаруживается личная выгода. Очень часто на фирме поощряется конкуренция между сотрудниками, как один из способов стимулирования. Именно поэтому американцы – ярко выраженные индивидуалисты и порой им очень сложно работать в команде.
Японские методы управления в корне отличны от американских. Это не значит, что японцы управляют более эффективно. Скорее можно сказать, что основные принципы американского и японского менеджмента лежат в разных плоскостях.
Японский менеджмент, основанный на коллективизме, использовал все морально психологические рычаги воздействия на личность. Прежде всего, это чувство долга перед коллективом, что в японском менталитете почти тождественно чувству стыда.
Чем отличается японский метод управления от методов, используемых в Америке? Прежде всего – своей направленностью: основным предметом управления в Японии являются трудовые ресурсы. Цель, которую ставит перед собой японский управляющий – повысить эффективность работы предприятия в основном за счет повышения производительности труда работников. Между тем в американском менеджменте основной целью является максимизация прибыли, т.е. получение наибольшей выгоды с наименьшими усилиями.
По-разному в американских и японских фирмах осуществляются контроль и оценка результативности действий работников:
- американская школа управления предусматривает четкие критерии оценки, которые в большинстве случаев можно выразить количественно (перед каждым работником ставятся четкие цели, которые необходимо достигнуть в определенный период);
- в японской фирме цели чаще всего формулируются в самом общем виде и отражают, главным образом, стратегию компании. Работа же сотрудников оценивается не за короткие, а за более длительные временные отрезки, и как правило, не на индивидуальной, а на групповой основе. Считается также, что понимая стратегические цели компании, каждый из сотрудников должен сам для себя ставить оперативные цели, реализация которых обеспечит достижение наиболее важных стратегических установок.
Основные подходы к управлению персоналом в американской и японской школе менеджмента представлены в табл. 1.
Таблица 1.
Подходы к управлению персоналом
| Подход к управлению персоналом | Американская модель | Японская модель |
| 1. «Человеческий капитал» | ü Малые вложения в обучение ü Сотрудника легче «купить» ü Обучение конкретным навыкам ü Формализованная оценка | ü Крупные вложения в обучение ü Сотрудника нужно «растить» ü Общее обучение ü Неформализованная оценка |
| 2. «Рынок трудовых ресурсов» | ü На первом месте внешние факторы ü Краткосрочный наем ü Специализированная лестница продвижения | ü На первом месте внутренние факторы ü Долгосрочный (пожизненный наем) ü Неспециализированная лестница продвижения |
| 3. «Преданность организации» | ü Прямые контакты по найму ü Внешние стимулы ü Индивидуальные рабочие задания ü Жесткая модель служебной карьеры | ü Подразумеваемые контракты ü Внутренние стимулы ü Групповая ориентация в работе ü Сложная лестница продвижения «Змея» |
| <== предыдущая лекция | | | следующая лекция ==> |
| Демографічна ситуація і міграційна активність населення | | | Сільськогосподарське виробництво у країнах ЄС |