Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Поручитель;
Дата добавления: 2015-10-01; просмотров: 612
|
|
Отношение относительной частоты к ширине интервала носит название плотности вероятности f(x)=mi / n dx = p*i / dx
Oсновные этапы построения гистограммы .
Для объяснения используем данные предыдущего примера.
1. Расчет количества интервалов
гдеn - число наблюдений. В нашем случае n = 100. Следовательно : 
2. Расчет ширины интервала dх :
, 
3. Составление интервального ряда :
| dх | 2.7-2.9 | 2.9-3.1 | 3.1-3.3 | 3.3-3.5 | 3.5-3.7 | 3.7-3.9 | 3.9-4.1 | 4.1-4.3 | 4.3-4.5 |
| m | |||||||||
| f(x) | 0.3 | 0.75 | 1.25 | 0.85 | 0.55 | 0.6 | 0.4 | 0.25 | 0.05 |
Гистограмма
ТОЧЕЧНАЯ ОЦЕНКА СЛУЧАЙНОЙ ВЕЛИЧИНЫ
(А.Н.Ремизов, 1987,стр.48-49, А.Н.Ремизов, 1999,стр.42-44, Г.Ф.Лакин, «Биометрия»,1990, стр. 99-106).
Предположим, что генеральная совокупность является нормальным распределением. Нормальное распределение полностью определено математическим ожиданием (средним значением) и средним квадратическим отклонением. Поетому если по выборке можно оценить, т.е. приближенно найти, эти параметры, то будет решена одна из задач математической статистики – определение параметров большого массива по исследованию егочасти.
Параметрыгенеральной совокупности можно указать по параметрам выборки с учетом ее объема n.
Если считать, что статистическое распределение является выборкой из некоторой генеральной совокупности, при этом 
, томожно заключить, что для этой генеральной совокупности приближенно:
ИНТЕРВАЛЬНАЯ ОЦЕНКА. ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ. ДОВЕРИТЕЛЬНАЯ ВЕРОЯТНОСТЬ.
(А.Н.Ремизов, 1987,стр.50-53, А.Н.Ремизов, 1999,стр.44-49, Г.Ф.Лакин, «Биометрия»,1990, стр. 106-110).
При достаточно большом объеме выборки можно сделать вполне надежные заключения о параметрах генеральной совокупности. Однако на практике часто имеют дело с выборками небольшого объема (n<30). При небольшом объеме выборки пользуются интервальными оценками. В этом случае указывается интервал (доверительный интервал).
Доверительный интервал – интервал, в котором с заданной доверительной вероятностью находится истинное значение случайной величины (среднее значение генеральной совокупности).
Доверительная вероятность – вероятность, с которой в заданном интервале (доверительном интервале) находится истинное значение случайной величины (среднее значение генеральной совокупности). Обычно в медико-биологических исследованиях доверительную вероятность принимают равной 0,95.
Доверительный интервал математически записывают так:
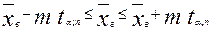, или
, где
- коэффициент Стьюдента (величина табличная, размерности не имеет),
a - доверительная вероятность,
n – объем выборки;
m – ошибка среднего.
Чтобы определить доверительный интервал, необходимо:
1. Вычислить среднее значение выборки 
;
2. Вычислить дисперсию для выборки 
;
3. Вычислить исправленную выборочную дисперсию:
4. Вычислить ошибку среднего 
.
ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
( Лобоцкая Н.Л. 1978, стр.389-391, Лакин Г.Ф., стр.111-133)
Ни одно исследование не обходится без сравнений. Сравнивать приходится данные опыта с контролем, эффективность действия препаратов, продуктивность одной группы животных с продуктивностью другой и т.д.
Обычно, между сравниваемыми данными всегда имеются различия. Иногда различиями пренебрегают и утверждают, что, в целом, данные контрольной группы совпадают с данными опытной группы, другими словами различия между полученными данными недостоверны. В другом случае различиями пренебречь нельзя и в таком случае говорят, что различия между полученными данными достоверны. В каком случае делается тот или иной вывод?
Введём несколько основных понятий:
1. 
- нулевая гипотеза, которая предполагает, что полученная в опыте разница между исследуемыми параметрами случайна;
2. 
- альтернативная гипотеза, которая противоречит нулевой и предполагает, что полученная в опыте разница между исследуемыми параметрами не случайна;
3. a- уровень значимости, равен вероятности ошибки, допускаемой при оценке принятой гипотезы (обычно равен0,05; 0,01; 0,001).
Принять или отклонить гипотезу можно после её проверки. Для этих целей служит величина, называемая статистическим критерием или просто критерием.
Критерии, которые вычисляются по исходным данным (выборкам) tф (фактические критерии) с р а в н и в а ю т с я с табличными критериямиtкр.
ОСНОВНОЙ ПРИНЦИП проверки статистических гипотез сводится к следующему:
| если фактически установленная величина tф превзойдёт или окажется равной критическому значению tкр, tф ³ tкр, то нулевую гипотезу отвергают. Если tф < tкр, принимают нулевую гипотезу. |
ПАРАМЕТРИЧЕСКИЕ И НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ РАЗЛИЧИЯ
( Лакин Г.Ф., стр.111-133)
В биометрии применяют два вида статистических критериев:
| 1. п а р а м е т р и ч е с к и е; |
| 2. н е п а р а м е т р и ч е с к и е. |
Применение параметрических критериев для проверки статистических гипотез основано на предположении о нормальном распределении (закон Гаусса) совокупностей, из которых взяты сравниваемые выборки. К параметрическим критериям относятся: 1.критерий Стьюдента; 2.критерий Фишера.
Однако не всегда исходные данные подчиняются нормальному закону распределения. Кроме того, исходные данные могут быть представлены качественно (например, наличие или отсутствие боли, восприятие света - есть или нет и т.д.). В таком случае используют непараметрические критерии: например, критерий знаков. Хотя непараметрические критерии можно использовать и для нормально распределённых величин. Но при нормальном распределении признака параметрические критерии обладают большей мощностью, чем непараметрические.
| <== предыдущая лекция | | | следующая лекция ==> |
| Прокурор; | | | Прокурор; |