
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Глухівські статті» Д.Многогрішного (1669 р.) 16
Дата добавления: 2015-10-12; просмотров: 769
|
|
Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой.
Направляющий вектор произвольной прямой в дальнейшем обозначается буквой а, его координаты — буквами l, т, т
а = {l; т; п}.
Если известна одна точка М0 (х0; у0; z0) прямой и направляющий вектор а = {l; т; п}. то прямая может быть определена (двумя) уравнениями вида:
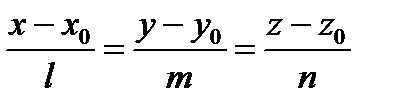 (1)
(1)
В таком виде уравнения прямой называются каноническими.
Канонические уравнения прямой, проходящей через две данные точки
М1 (х1; у1; z1 ) и М2 (х2; у2; z2) имеют вид:
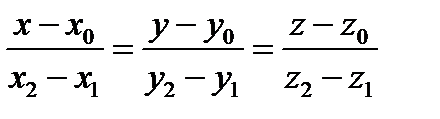 (2)
(2)
Обозначим буквой t каждое из равных отношений в канонических уравнениях (1); мы получим:
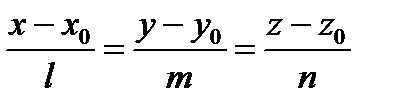
Отсюда 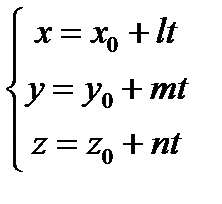
 (3)
(3)
Это — параметрические уравнения прямой, проходящей через точку М1 (х1; у1; z1 ) в направлении вектора а = {l; т; п}. В уравнениях (3) t рассматривается как произвольно изменяющийся параметр х, у, z — как функции от t; при изменении t величины х, у, z меняются так, что точка М (х; у; z) движется по данной прямой.
Если параметр t рассматривать как переменное время, а уравнения (3), как уравнения движения точки М, то эти уравнения будут определять прямолинейное и равномерное движение точки М. При t = 0 точка М совпадает с точкой M0. Скорость υточки М постоянна и определяется формулой
υ = 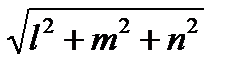
Пример 2. По координатам вершин пирамиды 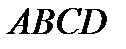 найти
найти
уравнение высоты, опущенной из вершины 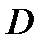 на грань
на грань 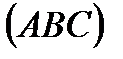 заданной уравнением
заданной уравнением 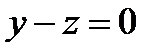 .
.
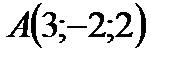 ;
; 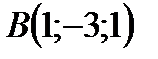 ;
;  ;
; 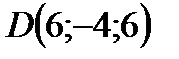 .
.
Решение: Составим уравнение высоты, опущенной из вершины 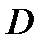 на грань
на грань 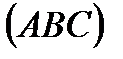 . Так как точка
. Так как точка 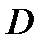 принадлежит высоте
принадлежит высоте 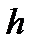 и высота
и высота 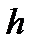 параллельна вектору нормали
параллельна вектору нормали 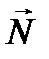 грани
грани 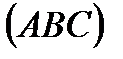 , то уравнение запишется в виде:
, то уравнение запишется в виде:
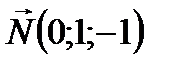 ,
, 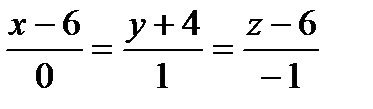 .
.
Ответ: 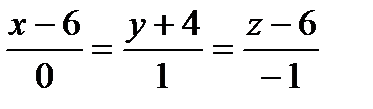 .
.
Решить задачи:
2.134.Составить канонические уравнения прямой, проходящей через точку
М 1 (2; 0; —3) параллельно:
1) вектору а = {2; —3; 5};
2) прямой 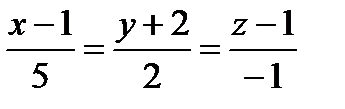
3) оси Ох; 4) оси Оу; 5) оси Oz.
2.135.Составить канонические уравнения прямой, проходящей через две данные точки:
1) (1; — 2; 1), (3; 1; —1); 2) (3; —1; 0),(1; 0, —3);
3) (0; —2; 3), (3; -2; 1); 4) (1; 2; —4), (—1; 2; —4).
2.136.Составить параметрические уравнения прямой, проходящей через точку
М1;( —1; —3) параллельно
1) вектору а = {2; —3; 4};
2) прямой 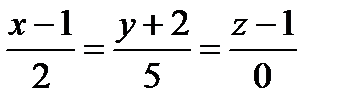
3) прямой х=3е— 1, у = — 2е+3, z = 5t + 2.
2.137.оставить параметрические уравнения прямой, проходящей через две данные точки: 1) (3; —1, 2), (2; 1; 1); 2) (1; 1; —2), (3; —1; 0); 3) (0; 0; 1), (0; 1; —2).
2.138.Через точки M 1 (—6; 6; —5) и М2(12; —6; 1) проведена прямая. Определить точки пересечения этой прямой с координатными плоскостями.
2.139.Даны вершины треугольника А(3; 6; —7), В(—5; 2; 3) и С(4; —7; —2). Составить параметрические уравнения его медианы, проведённой из вершины С.
2.140.Даны вершины треугольника А(1;—2;—4), В(3; 1; — 3) и С(5; 1; —7). Составить параметрические уравнения его высоты, опущенной из вершины В на противоположную сторону.
2.141.Составить канонические уравнения прямой, проходящей через точку М1(1; 3; —5) параллельно прямой
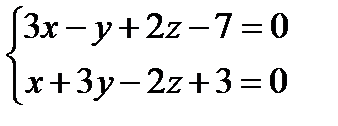
2.142.Составить канонические уравнения следующих прямых:
1) 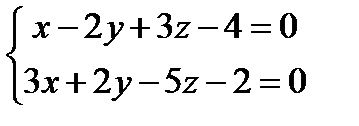 2)
2) 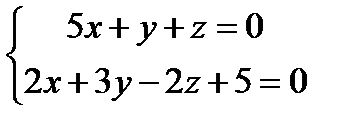
3) 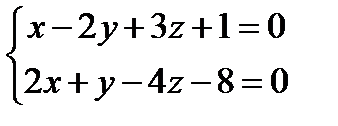
2.143.Составить параметрические уравнения следующих прямых:
1) 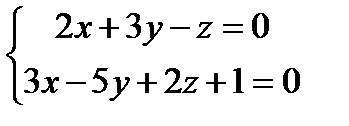 2)
2) 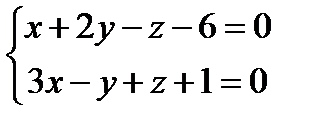
| <== предыдущая лекция | | | следующая лекция ==> |
| БЛАНК № 12. ХАРАКТЕРИСТИКА СПОРУДИ | | | ДЕКЛЯРАЦІЯ ЛАСКИ КОРОЛЯ Й. МИЛ. ДАНА НА ПУНКТИ ПРОШЕННЯ ВІЙСЬКА ЗАПОРОЗЬКОГО |