Властивості і приготування бетонної суміші.

Дата добавления: 2014-12-06; просмотров: 782

В соответствие со статьей 107 Конституции Российской Федерации федеральный закон обнародован 31 июля 2005 г.

Путеводитель по дисциплине

«Математический анализ»

для студентов 1 курса бакалавриата,

обучающихся по направлению «Менеджмент»

(2013-2014 уч. год)

Тема 1. Введение в анализ. Множества, функции

1. Понятие множества. Основные операции над множествами. Множество вещественных чисел. Числовые промежутки (с. 1-4).

2. Понятие функции (одной переменной). Способы задания функций. Область определения и множество значений функции (с. 4-5).

3. Сложная функция и обратная функция. Основные характеристики функций (с. 5-7).

4. Основные элементарные функции, их свойства и графики. Степенная, показательная и логарифмическая функции. Тригонометрические функции и обратные к ним (с. 7-10).

Тема 2. Теория пределов

1. Числовая последовательность. Способы ее задания. Монотонные последовательности, ограниченные последовательности (с. 11).

2. Предел последовательности и его свойства. Единственность предела. Ограниченность сходящейся последовательности (с. 12).

3. Основные теоремы о пределах (с. 23-26).

4. Бесконечно малые и бесконечно большие последовательности, их свойства (см. папку «Дополнительная литература», doc-файл «Числовые последовательности»).

5. Предел функции на бесконечности. Предел функции в точке. Односторонние пределы (с. 13-16).

6. Бесконечно малые и бесконечно большие функции, их свойства (с. 17-23).

7. Первый и второй замечательные пределы (с. 28-30).

8. Непрерывность функции в точке. Непрерывность суммы, разности, произведения и частного непрерывных функций. Непрерывность сложной функции. Непрерывность элементарных функций. Точки разрыва функции и их классификация. (с. 30-33).

9. Свойства функций, непрерывных на отрезке (с. 33-35).

10. Асимптоты графика функции (с. 87-88).

Тема 3. Дифференциальное исчисление функций одной переменной

1. Производная функции, определение и обозначения. Геометрический смысл производной. Уравнение касательной к графику функции. Дифференцируемость и дифференциал функции. Связь непрерывности и дифференцируемости функции (с. 47-50).

2. Правила дифференцирования суммы, разности, произведения и частного двух функций, сложной и обратной функций. Таблица производных основных элементарных функций (с. 50-55).

3. Дифференциал функции. Применение дифференциала для приближенных вычислений (С. 66-70).

4. Эластичность функции и ее применение в экономике (см. главу 7, параграф 7.10. учебника Н.Ш. Кремер. Высшая математика для экономического бакалавриата. – М.: Издательство Юрайт, 2012, 909 с.).

5. Локальный экстремум функции. Признак монотонности функции на интервале. Достаточное условие локального экстремума (с. 80-84).

6. Теорема Ферма. Теоремы Ролля и Лагранжа для дифференцируемых функций (С. 72-74).

7. Правило Лопиталя (с. 74-80).

8. Производные и дифференциалы высших порядков (с. 57-58, 71).

9. Формула Тейлора (Маклорена). Разложение функций 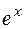, , 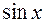, , 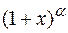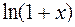по формуле Маклорена (с. 90-92).

10. Выпуклые (вогнутые) функции. Достаточные условия выпуклости функции. Необходимый и достаточный признаки точки перегиба (с. 86-87).

11. Общая схема исследования функции и построения ее графика (с. 88-90).

12. Наибольшее и наименьшее значения непрерывной функции на отрезке (с. 84-86).