
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
ПИТАННЯ 12. Релігійні уявлення Стародавнього Сходу
Дата добавления: 2015-10-15; просмотров: 796
|
|
|
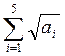 .
.
1) Ввести в блок А1:Е1 данные массива А;
2) задать имя массиву - А (Вставка/Имя/Присвоить);
3) в ячейку А2 ввести формулу массива: {=СУММ(КОРЕНЬ(A))}.
GПримечание. Формула должна вводиться как табличная, т.е. её ввод заканчивается нажатием комбинации клавиш
Ctrl+Shift+Enter.
GВывод. К массиву можно применить итоговую функцию, которая возвращает всего одно значение.
Но вводить такую формулу нужно как табличную.
Упражнение 6.3.2.
Имеются данные о месячном количестве осадков (в мм) по наблюдениям метеостанции за три года.
1) Подсчитать количество засушливых месяцев
(менее 10 мм в месяц).
2) Объёмы выпавших осадков в незасушливые месяцы
(более 10 мм в месяц).
3) Вычислить количество нормальных месяцев
(от 20 до 80 мм в месяц)
и объёмы выпавших осадков в эти месяцы.
Решение. Ввести в блок А1:D13 данные метеостанции;
задать имена массивам (например, г1998, г1999, г2000);
1) в ячейку Е4 ввести формулу: =СЧЁТЕСЛИ (г1998;"<10"), скопировать формулу в F4 и G4, затем автосуммой подсчитать итоги за три года.
2) в ячейку Е7 ввести формулу: =СУММЕСЛИ(г1998;">10"),скопировать формулу в F7 и G7, затем автосуммой подсчитать итоги за три года.
3) в ячейку Е10 ввести формулу:
{=СУММ ( ЕСЛИ(г1998>20; ЕСЛИ(г1998<80;1;0);0))},
а в Е12 - {=СУММ (ЕСЛИ (г1998>20; ЕСЛИ (г1998<80; г1998)))} (Ctrl+Shift+Enter !), затем скопировать и подвести итоги.
 Е F G H
Е F G H
Рис.17. Иллюстрация упражнения 6.3.2.
GПримечания.
1) С помощью функции СЧЕТЕСЛИ нельзя получить количество
месяцев, на протяжении которых количество осадков лежало
в диапазоне от 20 до 80 мм.
2) Использование формулы ЕСЛИ(И(В4>20,В4<80),1,0) при суммировании не приведет к успеху, т. к. функция И не применяется с итоговыми функциями.
GВывод. Чтобы подсчитать количество элементов, удовлетворяющих определённому критерию, нужно составить на основе вложенных функций ЕСЛИ
индикаторную функцию:
F(x)= 
а затем применить к ней итоговую функцию СУММ, введя как формулу массива.
Упражнение 6.3.3. В блоке А1:А20 записаны целые числа.
Сколько из них принимают наибольшее значение?
Решение: {=СУММ (ЕСЛИ (А = МАКС(А); 1; 0))},
где А - имя блока А1:А20.
Упражнение 6.3.4. В блоке А1:А10 записана числовая последовательность. Является ли она возрастающей?
Решение.
a) Нужно образовать блок, состоящий из первых разностей элементов исходного блока: А2:А10 - А1:А9 (здесь из А10 вычитается А9, из А9 вычитается А8 и т.д.);
b) составить блок из индикаторов положительных первых разностей ЕСЛИ (А2:А10 - А1:А9>0, 1, 0);
c) подсчитать количество ненулевых элементов в блоке индикаторов СУММ (ЕСЛИ ( А2:А10 - А1:А9>0, 1, 0)).
d) Если это количество равно размеру блока индикаторов (равному уменьшенному на 1 размеру исходного блока), то последовательность возрастающая, иначе — нет.
Окончательное решение дается формулой:
{=ЕСЛИ(СУММ(ЕСЛИ(А2:А10 - А1:А9>0,1,0))=СЧЕТ(А1:А10) -1, "возрастающая", "не является возрастающей")}
Задача 6.3.1. В А1:А5 и В1:В5 расположены векторы A и B. Вычислить квадрат расстояния между этими векторами, т.е. сумму квадратов разностей элементов этих векторов,
1) используя табличную формулу,
2) подобрав соответствующую функцию Excel.
Задача 6.3.2. Дан блок чисел А1:А20.
Подсчитать количество пар чисел, сумма которых равна заданному числу из В1.
Задача 6.3.3. Дан блок чисел А1:А10. Сколько из этих чисел больше своих "соседей", т.е. предыдущих и последующих чисел (крайние числа не учитывать)?
Задача 6.3.4. Дана последовательность ненулевых чисел в блоке С1:С11. Сколько раз в ней меняется знак (в по-следовательности 1, -34, 8, 14, -5 знак меняется три раза)?
Задача 6.3.5. Дан блок чисел Е1:Е11.
Сколько из этих чисел отличны от последнего числа?
Задача 6.3.6. Дан блок чисел F1:F10.
Подсчитать количество отрицательных чисел.
Задача 6.6.7. Дан блок чисел G2:G12, в котором имеется хотя бы одно отрицательное число. Найти величину наибольшего среди отрицательных чисел этого блока.
Задача 6.3.8. Дан блок чисел F1:F12. Вычислить сумму четных чисел из этого блока, нечетные игнорировать.
Задача 6.3.9. В блоке А1:А8 расположены числа. Найти порядковый номер того из них, которое наиболее близко по величине к числу, расположенному в ячейке В1. (Если таких чисел несколько, то найдите позицию первого такого числа.)
Задача 6.3.10. Дан блок чисел F1:F10. Найти в нём число, которое наиболее близко среднему арифметическому чисел этого блока.
| <== предыдущая лекция | | | следующая лекция ==> |
| ПИТАННЯ 11. Первісні вірування східних слов’ян | | | ПИТАННЯ 13. Релігії Стародавніх Греції і Риму |