
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Іnтеrмеzzo
Дата добавления: 2015-10-15; просмотров: 557
|
|
Рассмотрим график функции y = f(x) в окрестности фиксированной точки x0 (рис.5).
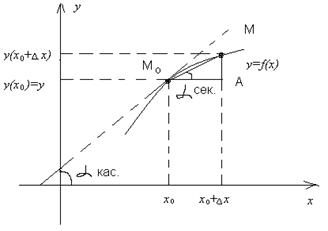
Рис. 5
Точка M0(x0;y(x0)) – фиксированная точка графика y = f(x). Точка M(x0+Dx;y(x0+Dx)) при различных значениях Dx – любая точка на графике. Если точка M приближается к точке M0 (при этом Dx ®0), то секущая линия M0M стремится к своему предельному положению, называемому касательной к линии y = f(x) в точке M0.
Рассмотрим D M0MA: tgaсек= 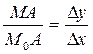 , aсек = угол наклона секущей M0M к оси Ox.
, aсек = угол наклона секущей M0M к оси Ox.
Перейдем к пределу при Dx ®0:

То есть y' (x0) = tg aкас => частное значение производной функции y = f(x) в точке x0 равно угловому коэффициенту касательной, проведенной к линии y = f(x) в точке M0(x0;y(x0)).
Тогда, используя уравнение прямой, проходящей через заданную точку M0(x0;y0) с известным угловым коэффициентом Kкас = y'(x0), можно записать уравнение касательной к линии y = f(x) в точке M0(x0;f(x0)):
y = f(x0) + f' '(x0)×(x-x0)
Аналогично, можно записать уравнение нормали – прямой, перпендикулярной касательной и проходящей через точку касания M0(x0;f(x0)):
y = f(x0) - 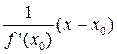 ,
,
используя условие перпендикулярности прямых: Kнорм = -  .
.
Таблица производных основных элементарных функций
1) 
Вывод: 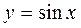 ;
; 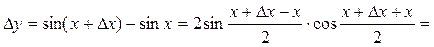
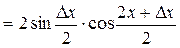

2)  ;
;
Вывод:  ;
; 
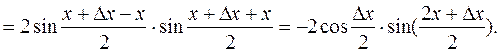

3) 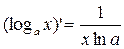
Вывод:  ;
; 

(используется второй замечательный предел и свойства логарифма).
4) 
Вывод: так как ln x = loge x, то, используя производную, для (loga x), можно записать: 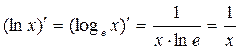
5) (c)' = 0
Вывод: y = c, Dy = y(x+Dx) - y(x) = c-c = 0 
Для остальных функций производные выводятся позже с помощью правил дифференцирования.
Таблица производных основных элементарных функций
1. (c)' =0
2. (xa) = a×xa-1
3. (ax)' = ax×lna, (a>0, a # 1)
4. (ex)' = ex
5. (logax)' =  , (a>0; a # 1)
, (a>0; a # 1)
6. (lnx)' = 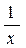
7. (sinx)' =cosx
8. (cosx)' = - sinx
9. (tgx)' = 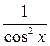
10. (ctgx)' = - 
11. (arcsinx)' = 
12. (arccosx)' = - 
13. (arctgx)' = 
14. (arcctgx)' = - 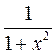
| <== предыдущая лекция | | | следующая лекция ==> |
| МИХАЙЛО КОЦЮБИНСЬКИЙ | | | Весь світ був як казка, повна чудес, таємнича, цікава й страшна. |