КОМБІНОВАНА ЗАГАЛЬНА АНЕСТЕЗІЯ

Дата добавления: 2014-12-06; просмотров: 601

Определение.Размещениями из n элементов по m ( ) называются такие соединения, каждое из которых содержит m элементов, взятых из данных n элементов, отличающиеся друг от друга либо элементами, либо порядком элементов.

Число всевозможных размещений из n по т обозначается ( А начальная буква французского слова “arranqement” - размещение)

Пример 1.Сколько двузначных чисел можно образовать из цифр 1. 2, 3. 4?

Решение.Составим двузначные числа, отличающиеся друг от друга хотя бы одной цифрой. Таких чисел будет шесть: 12, 13, 14, 23, 24, 34.В каждом из них поменяем порядок цифр: 12 - 21, 13 - 31, 14 - 41, 23 - 32, 24 - 42, 34 - 43.

Из четырех цифр получено 12 различных чисел, которые являются по определению размещениями,

Имеет место теорема.

Теорема. Число размещений из n элементов по m вычисляется по формуле

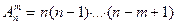(1)

Число размещений из n элементов по m равно произведению m целых последовательных чисел, большее из которых равно n.

Доказательство.Формула (1) справедлива для m =1, 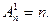Допустим, что она справедлива для m = k элементов. Докажем, что она справедлива и для

m = (k + 1) элементов.

Число размещений из n элементов по k будет равно

Каждая группа элементов из этого числа соединений состоит из k элементов,

К этой группе элементов добавим справа по одному элементу из остальных (n - k) элементов. Таким образом, с помощью этой одной группы мы получим (n - k) групп, состоящих уже из (k + 1) элемента.Но соединений, содержащих k элементов, будет 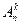штук. Следовательно, число размещений из элементов по (k + 1) будет равно

Таким образом, формула (1) справедлива и для m = k + 1.