МІСЦЕВА АНЕСТЕЗІЯ

Дата добавления: 2014-12-06; просмотров: 539

Определение. Сочетаниями из n элементов по m называются такие размещения из n элементов по m, которые отличаются друг от друга хотя бы одним элементом.

Число всех сочетаний из n элементов по m обозначается ( С - начальная буква французского слова combinaison - сочетание).

Пусть имеется n элементов. Из этих элементов составим сочетания по m элементов. Их число будет . Эти соединения будут отличаться друг от друга хотя бы одним элементом.

В каждом таком соединении сделаем перестановку. Число перестановок для одной группы будет P_n. Составим произведение , которое представляет собой число размещений из n элементов по m. Таким образом, будем иметь

Отсюда, учитывая формулы (1) и (2), получаем

(3)

Пример.Имеется семь деталей. Случайным образом выбираются три детали. Сколько вариантов выбора может быть при этом.

Решение.Число троек деталей будет равно числу сочетаний из семи по три. По формуле (3) будем иметь 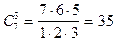вариантов.

Можно получить формулу числа сочетаний в другом виде:

(4)

Для числа сочетаний из n элементов по m имеет место равенство

Действительно, заменим в формуле (4) m на (n - m). Будем иметь

Это свойство применяется для вычисления числа сочетаний при достаточно близких значениях m и n.

Пример.Вычислить число сочетаний из 100 по 98.

Решение. .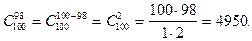

При практическом применении теории вероятностей часто приходится встречаться с задачами, в которых один и тот же опыт повторяется неоднократно. В результате каждого опыта может появиться или не появиться событие А. Причем, результат отдельного испытания нас может не интересовать. Необходимо знать лишь вероятность общего числа появления события А в результате серии опытов. Если, например, производится серия выстрелов по одной и той же мишени, то нас интересует не результат каждого выстрела, а общее число попаданий. В таких задачах требуется уметь определять вероятность заданного числа появления события А в серии опытов. Эта задача решается достаточно просто, когда испытания являются независимыми

Испытания называютсянезависимыми, если вероятность появления события А в каждом из испытаний не зависит от появления или не появления события А в других испытаниях.

Рассмотрим случай, когда независимые испытания проводятся в одинаковых условиях, Это означает, что вероятность появления события А в каждом испытании не меняется.

Пусть производится n независимых испытаний, в каждом из которых может появиться или не появиться событие А. При этом, вероятность появления события А в каждом испытании равна р, а вероятность не появления равна q = 1 - р. Требуется найти вероятность того, что в n испытаниях событие А появится ровно m раз.

Рассмотрим событие В_m, состоящее в том, что событие А появится ровно m раз в n испытаниях. Это событие может осуществляться различными способами. Разложим событие B_m на сумму произведений событий, состоящих в появлении или не появлении события А в отдельном испытании. Будем обозначать А_i появление события А в i-м испытании; - не появление события А в i - м испытании.

Каждый вариант появления события В_m ( каждый член суммы) должен состоять из m появлений события А и (n - m ) появлений события .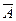

Таким образом

Число слагаемых, т.е. число всех комбинаций такого рода, отличающиеся одно от другого хотя бы одним номером числа испытаний, равно числу сочетаний из n элементов по m, . Другими словами число всех таких событий равно числу способов, какими можно из n испытаний выбрать m, в которых произошло событие А.

Вероятность каждой такой комбинации по теореме умножения вероятностей независимых событий равна р^mq^n-m. А так как комбинации событий между собой несовместны, то по теореме сложения, вероятность события В_m равна

Таким образом, можно дать следующую формулировку теоремы о повторении опытов.

Если производится n независимых испытаний, в каждом из которых событие А появляется с вероятностью р, то вероятность того, что событие А появится ровно m раз, выражается формулой

,

где q = 1 - p.

Полученная формула называется формулой Бернулли. Она верна и для крайних значений m = 0 и m = n. Если положить, как это принято, 0! = 1 и

Пример 1.Производится пять независимых выстрелов по цели, вероятность попадания в которую равны 0,2. Для разрушения цели достаточно трех попаданий. Найти вероятность разрушения цели.

Решение. Цель будет разрушена, если из пяти выстрелов будет 3, 4 или 5 попаданий. Это означает, что событие А - разрушение цели - является суммой трех несовместных событий, а именно, “три попадания при пяти выстрелах”, “четыре попадания при пяти выстрелах”, пять попаданий при пяти выстрелах”. Следовательно, вероятность разрушения цели равна сумме вероятностей этих событий.

Вопросы для самоконтроля: