Ключові поняття

Дата добавления: 2015-10-19; просмотров: 516

1.Даны матрицы

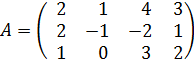и .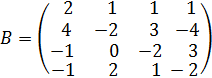

Найти ранг матрицы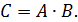

2. Методом обратной матрицы решить систему:

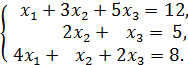
3. Установить, имеет ли однородная система

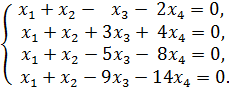
ненулевое решение. Найти общее решение системы.

4. Найти значение параметра α, при котором векторы 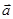и 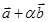перпендикулярны, если 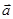= (6; –3; 5) и 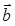= (–1; –3; 2).

5. Даны четыре вектора

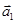=(2;1;0); 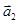=(1;–1;2); 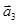=(2;2;–1); 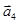=(3;7;– 7)

в некотором базисе. Показать, что векторы 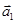, , 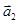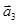образуют базис, и найти координаты вектора 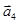в этом базисе.

6. Найти собственные значения и собственные векторы линейного оператора 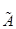, заданного матрицей А= .

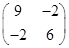7. а) Методом Лагранжа привести квадратичную форму

f(x_1, x₂)=4x₁²+3 x₂²+4x₁x₂

к каноническому виду (указать пример соответствующего преобразования координат).

б) По критерию Сильвестра исследовать на знакоопределенность квадратичную форму

f(x_1, x₂, x₃)=–2x₁²+5x₂²+3x₃² +2x₁x₂–2x₁x₃ –2x₂x_3.

1.Даны матрицы

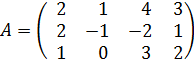и .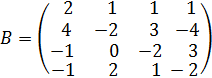

Найти ранг матрицы C=A∙B.

1)

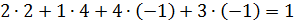
2)

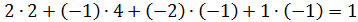
3)

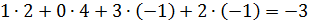
4)

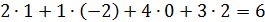
5)

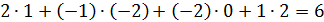
6)

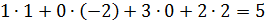
7)

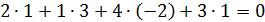
8)

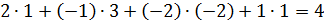
9)

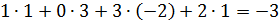
10)

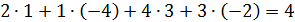
11)

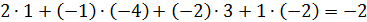
12)

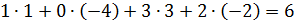
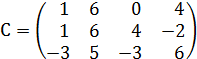
1. Вычесть из 2й строки 1ю.

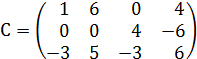
2. Домножаем 1ю строку на 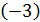и из 3й строки вычитаем 1ю.

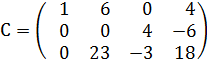
3. Меняем 2ю и 3ю строки местами.

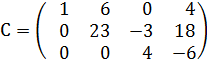
Количество линейно независимых строк = 3

Ответ: Ранг матрицы = 3.

2. Методом обратной матрицы решить систему:

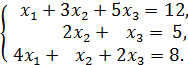
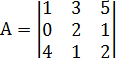
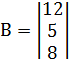
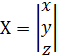
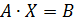
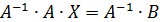
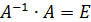
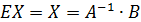
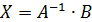
Находим определитель матрицы.

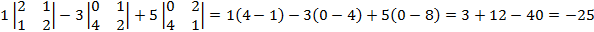
Определяем матрицу миноров матрицы А.

1)

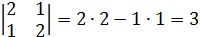
2)

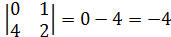
3)

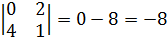
4)

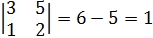
5)

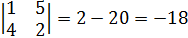
6)

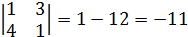
7)

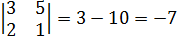
8)

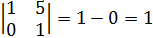
9)

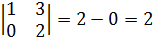
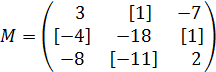
Меняем знаки у выделенных элементов, получаем :

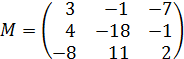
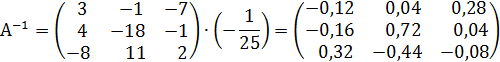
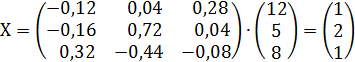
Ответ:X=1; Y=2; Z=1.

3. Установить, имеет ли однородная система

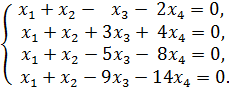
ненулевое решение. Найти общее решение системы.

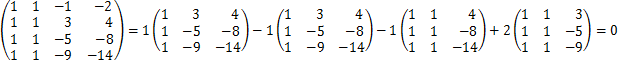
Преобразовываем матрицу до того момента, пока все показатели, находящиеся ниже диагонали, не будут = 0.

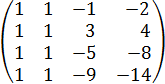
Из 2й строки вычитаем 1ю, получаем:

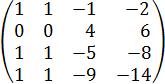
Из 3й строки вычитаем 1ю, получаем:

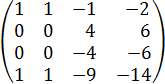
Из 4й строки вычитаем 1ю, получаем:

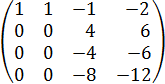
Умножаем 3ю строку на -1, получаем:

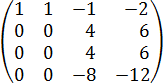
Из 3й строки вычитаем 2ю, далее меняем местами 3ю и 4ю строки, получаем:

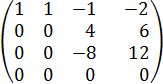
Делим 3ю строку на 2, далее умножаем на -1, вычитаем из 3й строки 2ю, получаем:

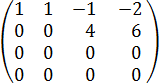
Делим 2ю строку на 2, получаем систему:

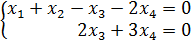
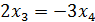
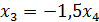
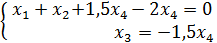
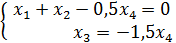
4. Найти значение параметра α, при котором векторы 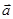и 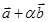перпендикулярны, если 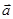= (6; –3; 5) и 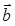= (–1; –3; 2).

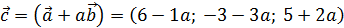
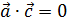
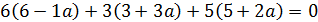
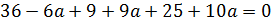
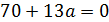
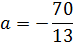
5. Даны четыре вектора

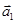=(2;1;0); 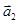=(1;–1;2); 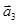=(2;2;–1); 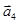=(3;7;– 7)

в некотором базисе. Показать, что векторы 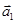, , 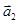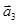образуют базис, и найти координаты вектора 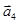в этом базисе.

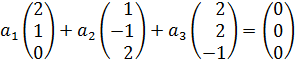
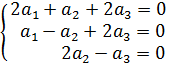
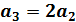
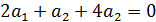
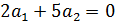
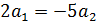
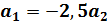
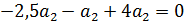
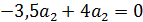
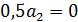
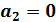
Показатели линейно независимы 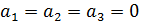следовательно образуют базис.

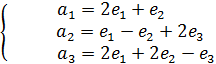
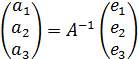
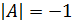(определитель матрицы).

Далее необходимо найти обратную матрицу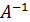

Вычисляем матрицу миноров матрицы A.

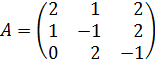
1)

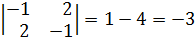
2)

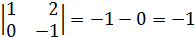
3)

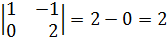
4)

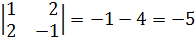
5)

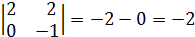
6)

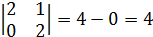
7)

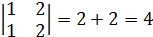
8)

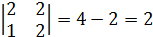
9)

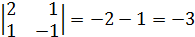
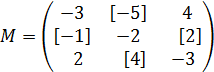
У выделенных элементов меняем знаки на противоположные.

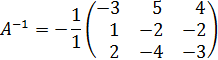
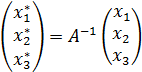
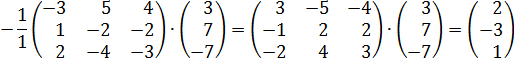
1)

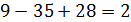
2)

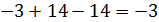
3)

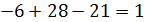
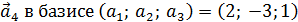
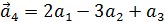
6. Найти собственные значения и собственные векторы линейного оператора 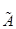, заданного матрицей А= .

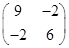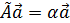
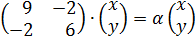
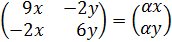
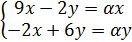
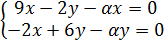
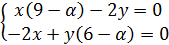
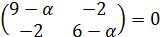
Находим собственные значения:

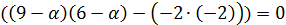
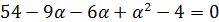
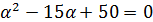
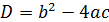
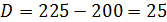
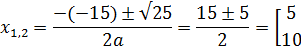
Далее для каждого собственного значения найдем его собственные векторы.

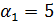
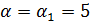
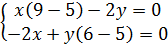
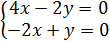
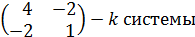
Решаем систему

Необходимо подобрать значение 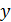так, чтобы 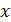было целым и положительным числом.

Пусть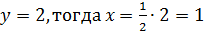

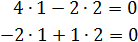
Таким образом, собственные векторы собственного значения 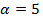представляют собой координаты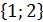

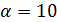
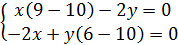
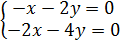
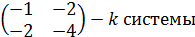
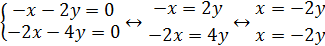
Необходимо подобрать значение 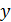так, чтобы 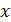было целым и положительным числом.

Пусть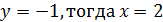

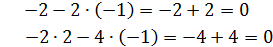
Таким образом, собственные векторы собственного значения 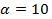представляют собой координаты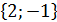

7. а) Методом Лагранжа привести квадратичную форму

f(x_1, x₂)=4x₁²+3 x₂²+4x₁x₂

к каноническому виду (указать пример соответствующего преобразования координат).

б) По критерию Сильвестра исследовать на знакоопределенность квадратичную форму

f(x_1, x₂, x₃)=–2x₁²+5x₂²+3x₃² +2x₁x₂–2x₁x₃ –2x₂x_3.

Проектирование механизированного процесса срезки растительного слоя без применения ЭВМ (примеры)

Растительный слой на строительной площадке срезают бульдозерами, автогрейдерами и скреперами (в зависимости от дальности перемещения), собирают в штабели и в последующем используют для работ по озеленению и благоустройству терри­тории.

В курсовом проекте необходимо выполнить технологический расчет процесса срезки растительного слоя. Процесс транспор­тирования растительного слоя за пределы строительной площадки не проектируют, но рассматривают как выполненный.