Методичні поради

Дата добавления: 2015-10-19; просмотров: 505

Выбор силовой схемы относится к плохо формализуемым задачам структурной оптимизации. Поэтому решения, связанные с выбором силовых схем, на практике зачастую принимаются эвристическими методами, на основании экспертных оценок, опыта и интуиции, а также с использованием результатов расчетов на упрощенных математических моделях (балка, пластина). Более достоверное исследование свойств объекта проектирования с применением метода конечных элементов (МКЭ) при этом производится лишь в конце процесса его разработки на стадии проведения поверочных расчетов. В такой ситуации существует вероятность того, что некоторые решения, связанные с выбором силовой схемы конструкции, могут оказаться неудачными. Попытки устранения недостатков в структуре конструкции на завершающих стадиях проектирования обычно требуют значительных дополнительных затрат времени и средств. Поэтому для снижения технического риска, повышения качества и эффективности процесса проектирования в работе [3] предложена стратегия формирования силовой схемы с привлечением МКЭ еще до начала полномасштабной разработки конструкции на этапе рабочего проектирования.

Связь между результатами расчетов конструкции по МКЭ и ее потребной массой удобно строить через специфический критерий "силовой фактор" G, который отражает одновременно величину и протяженность действия внутренних усилий в конструкции.

Для фермы, состоящей из n элементов, силовой фактор определяется следующим образом:

, (1)

где i - номер стержня,
N - усилие,
l - длина.

Для мембранной конструкции:

, (2)

где i - номер элемента,
R - эквивалентный поток усилий,
S – площадь в плане элемента.

Для трехмерной произвольной конструкции:

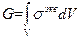, (3)

где ^экв - эквивалентное напряжение,
V - объем материала конструкции.

Свойства силового фактора подробно исследованы в работе [3]. Приведем ряд интересных свойств силового фактора, которые могут быть полезны для весовых оценок конструкций.

· G определяется силовой схемой конструкции. Для статически определимых конструкций величина G не зависит от соотношения жесткостей силовых элементов, а для статически неопределимых зависит очень слабо. Например, площади поперечных сечений некоторых элементов и внутренние усилия в них могут меняться в процессе оптимизации конструкции в несколько раз, в то время как G конструкции в целом изменяется только на несколько процентов.

· Теоретически необходимый объем материала полнонапряженной конструкции с определенной силовой схемой V_т может быть оценен через G и величину допускаемого напряжения с использованием расчета внутренних усилий для некоторого рационального распределения жесткостей элементов по простейшему соотношению

, (4)

где - допускаемое напряжение материала.

Действительно, для полнонапряженной фермы мы имеем

, (5)

где F_i - площадь поперечного сечения стержня.

Аналогичный результат можно получить для конструкций из мембранных элементов, если использовать в качестве меры внутренних усилий потоки эквивалентных усилий.

· Через V_т, плотность материала и коэффициент полной массы , который учитывает прирост массы за счет стыковочных и несиловых элементов в конструкции, за счет отклонений от оптимального распределения материала в пользу простоты и технологичности конструкций и т.п., можно вычислить реальную (практическую) массу конструкции:

(6)

или

, (7)

где - удельная прочность материала.

В весовой формуле (7) каждый из трех сомножителей определяет почти независимые от других свойства конструкции:

G - геометрия, силовая схема и нагрузки;

- прочность выбранного материала;

- конструктивно-технологическое совершенство. Этот коэффициент может быть определен из ретроспективного анализа уже построенного самолета, который целесообразно взять в качестве прототипа [3].

План решения задачи отыскания рациональной силовой схемы конструкции выглядит следующим образом.

1. В ограничения внешних размеров проектируемой конструкции вписывается непрерывная упругая среда (континуальная модель), которая включает в себя все возможные силовые схемы. Потенциально такое тело содержит внутри себя все мыслимые силовые схемы, в том числе и оптимальные с точки зрения передачи усилий или близкие к ним, которые могут быть образованы сгустками материала внутри допустимой геометрической области.

2. Решается задача об оптимальном распределении материала в исходной континуальной модели и таким образом находится теоретически оптимальная конструкция.

3. Анализируются главные пути передачи сил в теоретически оптимальной конструкции и с учетом конструктивных и технологических требований разрабатываются рациональные варианты силовых схем.

4. Через силовой фактор оценивается относительная эффективность разработанных силовых схем и близость их к идеалу – теоретически оптимальной конструкции.

В [3] рассмотрены детали, связанные с реализацией этого плана для различных типов конструкций, включая произвольные пространственные упругие системы.

Для решения задачи об оптимальном распределении материала в исходной континуальной модели можно использовать методы нелинейного математического программирования (прямые методы оптимизации) [5,6]. Если объект проектирования моделируется МКЭ, то за проектные переменные чаще всего принимаются параметры Х_i, описывающие размеры сечений конечных элементов (толщина пластины или площадь поперечного сечения стержня). При этом задача оптимизации конструкции обычно описывается большим количеством проектных переменных и функциональных ограничений, исчисляемым тысячами и даже десятками тысяч, что затрудняет подробное исследование области поиска и, следовательно, получение точных результатов. Это обстоятельство осложняется еще и тем, что методы нелинейного математического программирования используют "дорогую" (в смысле вычислительных затрат) процедуру анализа чувствительности ограничений на напряжения для множества точек конструкции по всем проектным переменным. Поэтому практический интерес представляет использование и развитие непрямых методов оптимизации упругих систем, которые могут обладать более высокой эффективностью за счет целенаправленного использования характерных свойств объекта проектирования.

В рамках непрямого подхода исходная задача оптимизации с ограничениями-неравенствами (эквивалентные напряжения во всех элементах конструкции не должны превышать допускаемых напряжений) заменяется косвенной. Постулируются необходимые условия, которым должна отвечать искомая конструкция, и строится процедура поиска этой конструкции. Условия оптимальности либо выводятся из математической постановки задачи, либо основываются на особенностях поведения, подмеченных для некоторых классов упругих систем. Для решения рассматриваемой задачи чаще всего используются критерии полнонапряженности и наибольшей жесткости конструкций.

Конструкция называется полнонапряженной (равнопрочной), если во всех ее элементах, в которых сечение больше минимально допустимого значения, реализуется предельное напряженное состояние хотя бы в одном из случаев нагружений. Для поиска полнонапряженного проекта (ПНП) используется классическая формула отношения напряжений:

Х_i⁽ⁿ⁺¹⁾ = Х_i⁽ⁿ⁾ max_j (s_ij)/ [s_i], j=1, 2, ..., s, (8)

где s_ij- эквивалентное напряжение в i-м элементе при j-м случае нагружения; [s_i] - допускаемое напряжение для i-го элемента; s - количество случаев нагружений; n - номер итерации.

Достоинства метода - простота и высокая эффективность. Концепция ПНП не включает в себя в явном виде целевую функцию. Тем не менее алгоритм, построенный на соотношении (8), часто приводит к "рациональному" проекту.

В основу концепции поиска наиболее жесткой конструкции (НЖК) [7] положена идея замены совокупности ограничений на напряжения для множества точек упругой системы одной интегральной характеристикой - потенциальной энергией. Обзор работ, посвященных оптимальному проектированию конструкций на основе минимизации энергии деформации, содержится в монографии [8].

В работе [7] ищется конструкция с минимальной энергией деформации при неизменном объеме материала. Среди множества вариантов распределения некоторого заданного количества материала внутри объекта проектирования определяется такой, при котором деформации конструкции (а, следовательно, и напряжения) будут наименьшими. При единственном случае нагружения в НЖК удельные энергии деформаций всех элементов конструкции, поперечные сечения которых больше минимально возможных, принимают одинаковые значения (разумеется, эти значения могут отличаться от допускаемых). Для перехода к реальной конструкции значения проектных переменных необходимо промасштабировать на коэффициент, который приведет максимальные напряжения конструкции в соответствие с условиями прочности. Отметим, что алгоритм поиска НЖК обладает высокой эффективностью. Как и в случае поиска полнонапряженного проекта, НЖК обычно удается определить за 5 -10 итераций.