Convergence tests for improper integrals

Дата добавления: 2015-10-19; просмотров: 533

Исторически первым научным представлением о свете являлась корпускулярная теория, получившая законченный вид в работах И. Ньютона (конец XVII в): свет рассматривался как поток малых материальных частиц – корпускул, движущихся в пустоте прямолинейно и равномерно со скоростью света, и замедляющихся в оптически плотных средах пропорционально их коэффициенту преломления. Подобное представление давало объяснение уже известным законам геометрической оптики и дисперсии, и тем самым позволило создать достаточно эффективную на первых порах теорию конструирования оптических приборов.

Но открытие в начале XIX века явлений интерференции и дифракции, а также поляризациявоскресило гипотезу Х. Гюйгенса, согласно которой свет представляет собой распространяющиеся механические колебания – волны - некой сплошной упругой среды ( светового эфира). На базе волновой гипотезы Т. Юнг объяснил явление интерференции; О. Френель создал эффективную теорию дифракции и вывел соотношения для отражения и преломления света на границе раздела оптических сред; Гаусс, Аббе, Зейдель и другие завершили классическую теорию оптических приборов. Последующее открытие электродинамики Максвелла и отождествление света с электромагнитными волнами, как тогда казалось, окончательно утвердило представление о свете как сугубо волновом процессе.

Однако никак не удавалось объяснить ряд явлений – отсутствие «эфирного ветра» в интерференционных экспериментах, характер излучения абсолютно черного тела и законы фотоэффекта. Разрешить проблему удалось А.Эйнштейну и М. Планку – так появились теория относительности и гипотеза квантов. Согласно теории относительности, процесс распространения электромагнитного поля это не вовлечение в колебательный процесс стационарной упругой среды – эфира, но реальное распространение в пространстве материи особого рода. Фундаментальное свойство любой материи – масса, и при распространении поля перенос энергии и массы неразрывно связаны. Исследования же процессов излучения и поглощения показали, что энергия и масса поля передается и распространяется дискретными порциями – квантами, причем кванты излучения демонстрировали свойства неделимости и пространственной локализации, подобно малым материальным частицам. Эти частицы были названы фотонами, от греческого слова φοτοσ – свет.

В 1925 году Л. де Бройль выдвинул радикальную гипотезу о волновой природе не только излучения, но любой материи, согласно которой на уровне атомных масштабов необходимо отказаться от представления о микрочастицах, элементарной формой материи являются поля, которые, распространяясь в форме волновых пакетов, в определенных условиях эксперимента способны демонстрировать корпускулярные свойства. Но более детальный анализ показал, что волновые пакеты де Бройля не обладают свойствами неделимости и локальности, неизменно присущими частицам в любых подобных экспериментах. Такое «странное», «необъяснимое» и «алогичное» поведение микрочастиц привело научное сообщество в конце 20-х годов XX века к осознанию того, что выхода из тупика не существует в рамках системы представлений и образов классической физики. Была создана новая физика – квантовая.

Принципиальное отличие квантовой физики от физики классической – наличие двух уровней теоретического представления реальности – формализма и интерпретации. Формализм – это собственно математический аппарат теории и алгоритм его применения. Интерпретация же обеспечивает связь между математикой формализма и физическим миром.

В классической механике, применительно к задаче движения материальной частицы, современный формализм выглядит следующим образом. Сначала определяется функция Гамильтона H, которая является выражением для полной энергии частицы в зависимости от ее координат q = (x, y, z)= (q1,q2 ,q3 ) и импульса p = (px , py , pz )= (p1, p2 , p3 ). Обычно функция Гамильтона представляет собой сумму кинетической и потенциальной энергии частицы.

Например, в случае движения частицы под действием силы тяжести:

,

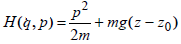при движении частицы с зарядом е в электрическом поле с потенциалом U:

.

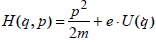Далее, записываются уравнения движения, являющиеся, по сути, формулировкой 2-го и 3-го законов Ньютона:

и закон сохранения энергии:

Если дополнить эти дифференциальные уравнения начальными или граничными условиями, то полученные частные решения – векторные функции времени q(t), описывают геометрическое место точек центра масс исследуемой частицы, и называются ее траекториями. Дифференцируя траекторию по времени и умножая на массу, можно легко получить также и значения импульса частицы в любой момент времени, далее с помощью известных формул - мгновенные значения кинетической и потенциальной энергий частицы. Тем самым, в классической механике из факта наличия определенной траектории однозначно следует, что имеется и вся остальная информация о параметрах движения частицы.

Формализм квантовой механики существенно отличается от изложенного только что классического. В первую очередь, в нем отсутствуют функции, описывающие интуитивно-очевидные физические свойства и параметры частицы – координату, скорость, импульс, энергию и т.п. Вместо них вводятся операторы, воздействующие на особую комплексную функцию состояния, или пси-функцию, зависящую от координат и времени: Ψ (q,t). Операторы бывают типа умножения, например, оператор координаты и потенциальной энергии ; дифференциального типа, например, оператор импульса ; и смешанного типа – оператор полной энергии (оператор Гамильтона, или Гамильтониан):

Основным уравнением, вместо уравнений движения, является уравнение Шредингера:

Неизвестной функцией здесь является функция состояния Ψ , логически занимающая место траектории в классической механике. Но, если в классической механике сама траектория и получаемые из нее прочие величины уже являются интуитивно-понятными, базовыми физическими параметрами и характеристиками движения, то результат применения квантового формализма – функция состояния, нуждается в дополнительной интерпретации, связывающей ее с реальными наблюдаемыми физическими величинами.

Первоначально создатель данного формализма Э. Шредингер предполагал, что функции состояния описывают волны плотности материи, подобно волновым пакетам де Бройля, но такая интерпретация также оказалась несостоятельной по тем же причинам – нарушался принцип локальности частиц. В конце концов, трудом многих ученых адекватная интерпретация была создана, но ценой отказа от интуитивных концепций физики микромира и пересмотра всего философского представления человечества о материи и физической реальности.

Основных положений интерпретации квантовой механики существует три: статистическая интерпретация функции состояния (М. Борн, 1926); принцип неопределенности (В. Гейзенберг, 1927); принцип дополнительности (Н. Бор, 1928).

Согласно статистической интерпретации Борна, функция состояния (а точнее, квадрат ее модуля) описывает не распределение плотности массы частицы в пространстве, а распределение плотности вероятности нахождения частицы в данной точке пространства в данный момент времени. Тем самым снимается проблема нелокальности, свойственная ранним интерпретациям де Бройля и Шредингера. Соответственно, идея о волнах материи отвергается, и квантовая частица объявляется корпускулой, но принципиально отличной от классической корпускулы в ньютоновском смысле, а именно – квантовая частица не имеет траектории. Ее «движение» имеет вероятностный, статистический характер не из-за отсутствия начальной информации о параметрах, но является фундаментальным свойством, потому сам термин «движение» применительно к квантовой частице применяется условно и взят в кавычки, так как из-за отсутствия определенной траектории классическое определение данного термина теряет смысл. Соответственно, после решения уравнения Шредингера и нахождения функции состояния, вместо утверждения, что «частица в момент времени t находится в точке q», привычного в классической механике, утверждается, что «в момент t существует вероятность обнаружить частицу в объеме V, равная:

Принцип неопределенности Гейзенберга устанавливает особую роль канонически-сопряженных величин. В классической механике, как уже было сказано выше, наличие точно определенной траектории частицы позволяет столь же точно определить все параметры ее движения и связанные с ними физические величины. В квантовой же механике утверждается, что для каждой канонически сопряженной пары величин погрешности их определения, как экспериментального, так и теоретического, не являются произвольными, а подчиняются соотношению:

Практически значимые варианты этого соотношения связывают координату и импульс частицы: Δq⋅Δp ≥ η/ 2 ; полную энергию системы и время ее измерения: ΔE⋅Δt ≥ η/ 2; и, в квантовой оптике, число фотонов в системе n и фазу Φ соответствующей им волны: Δn⋅ΔΦ ≥ 2π.

Принцип дополнительности Бора подводит общую базу под известные свойства квантовой частицы – отсутствие траектории, невозможность точного измерения канонически сопряженных величин и одновременную демонстрацию корпускулярных и волновых свойств. Все это является следствием того факта, что, во-первых, любой натурный эксперимент или его теоретическое моделирование предусматривает наличие макроскопических, «классических» объектов – измерительной аппаратуры и наблюдателя, которые так или иначе физически взаимодействуют с объектом наблюдения. В классической физике энергия этого взаимодействия считается пренебрежимо малой и не влияющей на результат эксперимента. В микромире же энергия процесса взаимодействия аппаратуры и объекта может многократно превышать энергию изучаемых процессов. Этим и объясняется принципиальная неопределенность и вероятностный характер квантовых процессов для макроскопических наблюдателей, поскольку измерительная процедура, нацеленная на определение какой-либо величины, вследствие взаимодействия с объектом наблюдения неминуемо изменит сам объект и «испортит» его прочие параметры, сделав невозможным их точное определение одновременно с основной величиной. Корпускулярно-волновой дуализм имеет ту же природу.

Квантовые объекты, которые по своей сути не являются ни корпускулами, ни волнами, будучи вовлечены в определенную экспериментальную схему, на макроскопическом уровне демонстрируют свойства макрообъектов - «корпускул» или «волн», в соотношении, определенными условиями эксперимента. Причем корпускулярные и волновые свойства находятся в отношении «дополнения» друг к другу (отсюда и название принципа), то есть, чем в большей степени демонстрируются волновые свойства, тем меньше корпускулярные, и наоборот.

В квантовой электродинамике и оптике этот принцип применяется следующим образом. Поскольку число фотонов в системе n и фаза Φ соответствующей им волны являются сопряженными величинами и связаны соотношением неопределенности Δn⋅ΔΦ≥2π, то если в эксперименте или теоретическом анализе точно фиксируется число фотонов, фаза оказывается неопределенной и волновые представления об электромагнитном поле неприменимы. Обычно это актуально, когда само число фотонов относительно невелико. В большинстве же обычных задач оптики число n принимающих участие в наблюдаемом процессе фотонов огромно, и, соответственно, весьма велико и его среднее отклонение Δn. В этом случае фаза вполне определена, и поле можно рассматривать как волну.