
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
тільки за згодою Держави прапору судна
Дата добавления: 2015-10-19; просмотров: 712
|
|
Теорема Вариньона:
| Если система сил, приложенных к абсолютно твердому телу, имеет равнодействующую, то момент равнодействующей относительно произвольного центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси). |
Векторная запись теоремы: 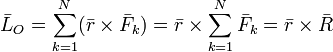 .
.
Билет4.Плоская система сил. Приведение плоской системы сил к простейшему виду. Равновесие плоской системы сил.
Если все силы, действующие на твердое тело, лежат на одной плоскости, выберем систему координат xOy в плоскости действия сил (рисунок 2.1). В этом случае обнаружим, что
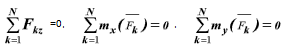
Далее, вспомнив определение момента силы относительно оси, замечаем, что сумма моментов всех сил относительно оси z равна алгебраической сумме моментов этих сил относительно начала координат, т.е. точки О. В результате останутся следующие три аналитические условия равновесия:
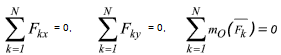
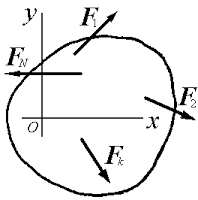
Рисунок 2.
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из координатных осей x и y и сумма моментов всех сил относительно любой точки, лежащих в плоскости действия сил, были равны нулю.
Произвольной плоской системой сил называется совокупность сил, линии действия которых находятся в одной плоскости.
Главным вектором системы сил называется вектор, равный векторной сумме этих сил:
R = ΣFk.
Главным моментомсистемы сил относительно точки O тела, называется вектор, равный векторной сумме моментов всех сил системы относительно этой точки:
Mo = ΣMo(Fk).
| <== предыдущая лекция | | | следующая лекция ==> |
| Процедури контролю за доставкою суднових запасів | | | Одеса 2009 |