Черт. 2горизонтальные и вертикальные составляющие: —H, —V, Н+dН, V+ dV, 0 и mg. Условие равновесия можно записать по составляющим:
Из первого равенства получаем:
т. е. горизонтальная составляющая натяжения в любой точке нити одна и та же. Из второго равенства получаем:
Так как натяжение направлено по касательной к кривой, изображающей нить, то, обозначив через α угол между натяжением в точке А и положительным направлением оси ОХ, имеем из чертежа 2:
где у — переменная ордината кривой. Отсюда, дифференцируя полученное соотношение и помня, что H — постоянная, получаем:
Подставляем полученное выражение для dV в (14):
Пишем для дифференциала дуги ds известное выражение из интегрального исчисления
и подставляем его в (15):
Отсюда, обозначив
Получено опять дифференциальное уравнение, но на этот раз второго порядка, из которого надо определить ординату кривой у как функцию абсциссы х, т. е. получить уравнение кривой, по которой происходит провисание. Нахождение у из уравнения (16) мы разберем в главе II, § 2. Очевидно, что процесс интегрирования даст опять произвольные постоянные, и поэтому выясним сразу, какие есть условия в нашей задаче, позволяющие определить числовые значения этих постоявших. По выбранному расположению кривой в координатной системе имеем: у = а при х = 0 и у' = 0 при х = 0 (так как производная равна нулю в точке минимума). Это и есть начальные условия нашей задачи. Замечание. При решении этой задачи мы рассматривали бесконечно малый элемент кривой и бесконечно малые приращения тех величин, которые нас интересовали в этой задаче. При решении предыдущих задач мы этого не делали, но это было потому, что там мы использовали уже готовые понятия скорости изменения величины и углового коэффициента касательной, а эти понятия сами в свое время были получены из рассмотрения бесконечно малых элементов. Замена приращений функций дифференциалами, которой мы пользовались в выкладках при решении пятой задачи, сводится по существу к отбрасыванию бесконечно малых слагаемых высшего порядка малости, что, конечно, облегчает выкладки. Можно доказать, что это отбрасывание не влияет на характер получаемого результата, т. е. полученное дифференциальное уравнение такое же, какое бы получилось, если бы и не заменяли приращении дифференциалами и не отбрасывали бесконечно малые слагаемые высшего порядка малости. Действительно, пусть, например, дифференциальное уравнение первого порядка вида:
получено такими рассуждениями, при которых бесконечно малые приращениязаменялись соответствующими дифференциаламии отбрасывались бесконечно малые слагаемые порядкавысшего, чем ∆ х. Если такой заменыи отбрасывания таких слагаемых в выкладках в процессе составления дифференциального уравнения непроизводить, то кмоменту получения окончательного уравнения накопится много слагаемых порядка малости выше ∆ х; сосредоточим все такие слагаемые в правой части уравнения и обозначим их сумму через α. Тогда полученное уравнение будет иметь вид:
Разделим обе части уравнения на ∆ х:
при ∆ х → 0 и
Так как Приведенные задачи показывают, насколько широк и разнообразен круг вопросов, требующих для своего изучения решения дифференциальных уравнений.
|

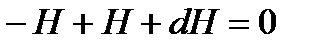 и
и  .
. ,
,  ,
, . (14)
. (14)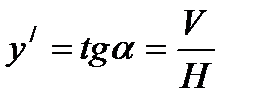 ,
, .
. . (15)
. (15)
 .
. , получаем:
, получаем: . (16)
. (16)
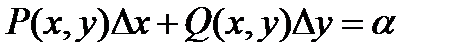 .
. ;
; → 0 (так как α высшего порядка малости, чем ∆ х ) и поэтому в результате предельного перехода получим:
→ 0 (так как α высшего порядка малости, чем ∆ х ) и поэтому в результате предельного перехода получим: .
. , то это уравнение действительно совпадает с уравнением, полученным выше первым способом.
, то это уравнение действительно совпадает с уравнением, полученным выше первым способом.


