Определение. Уравнение вида
 (1.43)
(1.43)
где 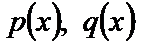 – непрерывные на некотором интервале
– непрерывные на некотором интервале  функции,
функции,  действительное число, отличное от 0 и 1, называется уравнением Бернулли.
действительное число, отличное от 0 и 1, называется уравнением Бернулли.
Делением обеих частей на  и подстановкой
и подстановкой 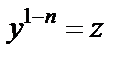 , где
, где  новая неизвестная функция, это уравнение приводится к линейному уравнению
новая неизвестная функция, это уравнение приводится к линейному уравнению
 .
.
Заметим, что при делении обеих частей уравнения (1.43) на 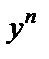 при
при  возможна потеря решения
возможна потеря решения  . Это решение является частным, если
. Это решение является частным, если  , и особым, если
, и особым, если  .
.
Пример 1 Решить уравнение
 .
.
Решение. Обе части уравнения разделим на  , тогда будем иметь:
, тогда будем иметь:
 . (1.44)
. (1.44)
Положим  , откуда
, откуда  . В силу введенной подстановки уравнение (1.44) можно записать следующим образом:
. В силу введенной подстановки уравнение (1.44) можно записать следующим образом:
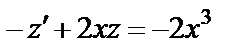
или
 (1.45)
(1.45)
Последнее уравнение – линейное относительно функции 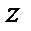 . Его общее решение есть
. Его общее решение есть
 ,
,
где  произвольная константа (см. п.1.4., пример 1). Отсюда, учитывая, что
произвольная константа (см. п.1.4., пример 1). Отсюда, учитывая, что  , записываем общий интеграл исходного уравнения
, записываем общий интеграл исходного уравнения
 .
.
Так как показатель степени  в правой части нашего уравнения равен 2, то потерянное при интегрировании решение
в правой части нашего уравнения равен 2, то потерянное при интегрировании решение  является частным.
является частным.
Замечание. При интегрировании уравнения Бернулли можно также непосредственно применить подстановку  или метод вариации произвольной постоянной.
или метод вариации произвольной постоянной.
Пример 2 Проинтегрировать уравнение
 . (1.46)
. (1.46)
Решение. Уравнение (1.46) – это уравнение Бернулли. Положим  , тогда (1.46) запишется в виде
, тогда (1.46) запишется в виде
 .
.
или
 .
.
Функцию  выберем так, чтобы
выберем так, чтобы  . Например, пусть
. Например, пусть  . Подставив
. Подставив  вместо
вместо  в последнее уравнение и учитывая, что
в последнее уравнение и учитывая, что  , для определения
, для определения  будем иметь уравнение
будем иметь уравнение
 . (1.47)
. (1.47)
Последнее уравнение – это уравнение с разделяющимися переменными, его общий интеграл есть
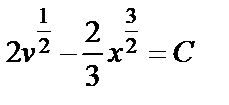 ,
,
откуда
 ,
,
где  произвольная константа. Следовательно, общее решение ОДУ (1.46) есть
произвольная константа. Следовательно, общее решение ОДУ (1.46) есть
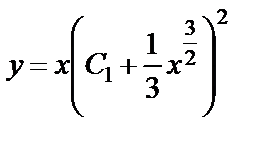 . (1.48)
. (1.48)
Заметим, что при интегрировании уравнения (1.47) методом разделения переменных мы теряем решение  , это ведет к потере решения
, это ведет к потере решения  уравнения (1.46). Так как в правой части (1.46) стоит степень
уравнения (1.46). Так как в правой части (1.46) стоит степень 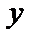 с показателем
с показателем  , то теряемое решение является особым.
, то теряемое решение является особым.
Рассмотрим другой способ решения уравнения (1.46), а именно проинтегрируем его методом вариации произвольной постоянной. Запишем однородное уравнение, соответствующее (1.46):
 .
.
Его общее решение есть 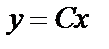 . Пусть С= С (х), тогда общее решение (1.41) будем искать в виде
. Пусть С= С (х), тогда общее решение (1.41) будем искать в виде
 . (1.49)
. (1.49)
Подставив  и
и  в уравнение, будем иметь
в уравнение, будем иметь
 ,
,
или
 .
.
Проинтегрировав последнее уравнение, находим
 ,
,
или
 ,
,
где  произвольная константа,
произвольная константа,  . Подставляя С (х) в (1.49), получаем общее решение уравнения (1.49) в форме (1.48)
. Подставляя С (х) в (1.49), получаем общее решение уравнения (1.49) в форме (1.48)
 .
.

 (1.43)
(1.43)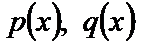 – непрерывные на некотором интервале
– непрерывные на некотором интервале  функции,
функции,  действительное число, отличное от 0 и 1, называется уравнением Бернулли.
действительное число, отличное от 0 и 1, называется уравнением Бернулли. и подстановкой
и подстановкой 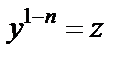 , где
, где  новая неизвестная функция, это уравнение приводится к линейному уравнению
новая неизвестная функция, это уравнение приводится к линейному уравнению .
.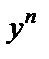 при
при  возможна потеря решения
возможна потеря решения  . Это решение является частным, если
. Это решение является частным, если  , и особым, если
, и особым, если  .
. .
. , тогда будем иметь:
, тогда будем иметь: . (1.44)
. (1.44) , откуда
, откуда  . В силу введенной подстановки уравнение (1.44) можно записать следующим образом:
. В силу введенной подстановки уравнение (1.44) можно записать следующим образом: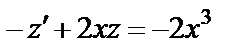
 (1.45)
(1.45)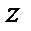 . Его общее решение есть
. Его общее решение есть ,
, произвольная константа (см. п.1.4., пример 1). Отсюда, учитывая, что
произвольная константа (см. п.1.4., пример 1). Отсюда, учитывая, что  , записываем общий интеграл исходного уравнения
, записываем общий интеграл исходного уравнения .
. в правой части нашего уравнения равен 2, то потерянное при интегрировании решение
в правой части нашего уравнения равен 2, то потерянное при интегрировании решение  является частным.
является частным. или метод вариации произвольной постоянной.
или метод вариации произвольной постоянной. . (1.46)
. (1.46) , тогда (1.46) запишется в виде
, тогда (1.46) запишется в виде .
. .
. выберем так, чтобы
выберем так, чтобы  . Например, пусть
. Например, пусть  . Подставив
. Подставив  вместо
вместо  в последнее уравнение и учитывая, что
в последнее уравнение и учитывая, что  , для определения
, для определения  будем иметь уравнение
будем иметь уравнение . (1.47)
. (1.47)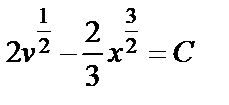 ,
, ,
, произвольная константа. Следовательно, общее решение ОДУ (1.46) есть
произвольная константа. Следовательно, общее решение ОДУ (1.46) есть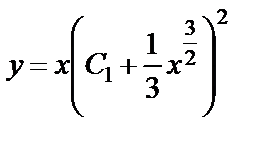 . (1.48)
. (1.48) , это ведет к потере решения
, это ведет к потере решения  уравнения (1.46). Так как в правой части (1.46) стоит степень
уравнения (1.46). Так как в правой части (1.46) стоит степень 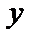 с показателем
с показателем  , то теряемое решение является особым.
, то теряемое решение является особым. .
.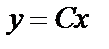 . Пусть С= С (х), тогда общее решение (1.41) будем искать в виде
. Пусть С= С (х), тогда общее решение (1.41) будем искать в виде . (1.49)
. (1.49) и
и  в уравнение, будем иметь
в уравнение, будем иметь ,
, .
. ,
, ,
, произвольная константа,
произвольная константа,  . Подставляя С (х) в (1.49), получаем общее решение уравнения (1.49) в форме (1.48)
. Подставляя С (х) в (1.49), получаем общее решение уравнения (1.49) в форме (1.48) .
.


