Решение одной задачи выпуклого программирования.Рассмотрим следующую задачу оптимизации
В (28) Очевидно, что (28) – задача со строго выпуклыми функциями и линейными ограничениями и имеет форму основной задачи выпуклого программирования с равенствами. Для этой задачи справедлива теорема Куна-Таккера, причем
Составим условие стационарности:
Отсюда получаем:
Нетрудно убедиться, что функция
Составляем условие стационарности (32)
Отсюда находим оптимальный план (31), получаем:
По теории двойственности тогда существует оптимальный план и прямой задачи, которая совпадает с (28) и он имеет вид:
Таким образом, теория двойственности позволяет для задачи (28) сразу получить оптимальный план в явной форме. Задача (28)относится к задачам квадратичного программирования, то есть к задачам с квадратичной целевой функцией и линейными ограничениями.
|

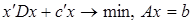 . (28)
. (28) – симметричная
– симметричная 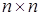 матрица,
матрица,  .
.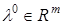 . Построим для задачи (28) функцию Лагранжа.
. Построим для задачи (28) функцию Лагранжа.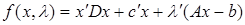 и будем строить двойственную функцию:
и будем строить двойственную функцию:  . Поскольку функция Лагранжа
. Поскольку функция Лагранжа 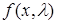 при
при  строго выпукла, то
строго выпукла, то  достигается в стационарной точке, то есть там, где
достигается в стационарной точке, то есть там, где 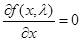 (29)
(29)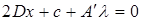
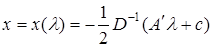 (30)
(30) . И построим двойственную задачу:
. И построим двойственную задачу: 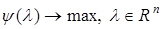 (31)
(31) является строго вогнутой относительно
является строго вогнутой относительно  (для этого нужно взять вторую производную по
(для этого нужно взять вторую производную по 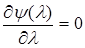 (32)
(32)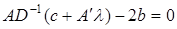 .
.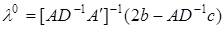 – оптимальный план (31).
– оптимальный план (31).



