Пусть дана задача:  (1)
(1)
Первоначально Лагранж считал, что в теореме 1 можно для любых задач положить  , то есть правило справедливо для классической функции Лагранжа. Однако это было ошибкой. Покажем это на следующем примере.
, то есть правило справедливо для классической функции Лагранжа. Однако это было ошибкой. Покажем это на следующем примере.
Оказывается, что из задачи (1) можно выделить такой подкласс, который с одной стороны является очень широким (практически все важные и интересные задачи принадлежат ему), а с другой стороны, для которого правило Лагранжа справедливо в классической форме.
Определение. Некоторый план задачи (1)  (здесь необязательно оптимальный) будем называть обыкновенным, если вектора
(здесь необязательно оптимальный) будем называть обыкновенным, если вектора
 (7)
(7)
линейно независимы  .
.
Теорема 2 (Классическое правило множителей Лагранжа). Если  – обыкновенный локально-оптимальный план задачи (1), то всегда найдётся такой единственный классический вектор Лагранжа
– обыкновенный локально-оптимальный план задачи (1), то всегда найдётся такой единственный классический вектор Лагранжа 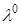 , что выполняется условие:
, что выполняется условие:
 (8)
(8)
Доказательство. Пусть  – обыкновенный локально-оптимальный план. В силу локальной оптимальности для него справедлива теорема 1. В частности, условия (5) или (5*). Докажем, что в силу обыкновенности в (5*) множитель
– обыкновенный локально-оптимальный план. В силу локальной оптимальности для него справедлива теорема 1. В частности, условия (5) или (5*). Докажем, что в силу обыкновенности в (5*) множитель  . Предположим противное, то есть
. Предположим противное, то есть  . Тогда из условия (5*) получаем
. Тогда из условия (5*) получаем
 , (9)
, (9)
в котором не все множители  нулевые. Тогда (9) означает линейную зависимость векторов
нулевые. Тогда (9) означает линейную зависимость векторов  и противоречит обыкновенности
и противоречит обыкновенности  .
.
Итак,  . Разделим тогда выражение (5*) на
. Разделим тогда выражение (5*) на 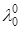 и переобозначим:
и переобозначим:  , тогда придём к условию (8).
, тогда придём к условию (8).
Докажем единственность 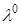 . Предположим противное. Найдётся ещё один вектор Лагранжа
. Предположим противное. Найдётся ещё один вектор Лагранжа  такой, что
такой, что 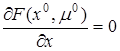 . Вычитая из этого равенства равенство (8), придём к
. Вычитая из этого равенства равенство (8), придём к  , причём не все коэффициенты
, причём не все коэффициенты  . Это означает линейную зависимость векторов (7) и снова противоречит обыкновенности
. Это означает линейную зависимость векторов (7) и снова противоречит обыкновенности  .
.
Ч.т.д.
Обсуждение. Теорема 1 и теорема 2 вместе составляют так называемый принцип Лагранжа снятия ограничений в задаче (1). Согласно которому и оптимальный план, и все локально оптимальные планы должны удовлетворять либо (5), либо (8), и поэтому должны находится среди решений систем
 (10)
(10)
для обыкновенного плана  и
и
 (11)
(11)
если  не является обыкновенным.
не является обыкновенным.
Каждая из систем (10) и (11) представляет собой систему  уравнений относительно
уравнений относительно  неизвестных
неизвестных 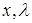 . Среди решений этих систем и только среди них нужно искать
. Среди решений этих систем и только среди них нужно искать  .
.
Определение. Задача (1) называться нормальной, если  – обыкновенный оптимальный план.
– обыкновенный оптимальный план.
Определение. Пара  называется условно-стационарной точкой задачи (1),если она является решением системы (10).
называется условно-стационарной точкой задачи (1),если она является решением системы (10).
Принцип Лагранжа или теорему 2 можно переформулировать:
Если  – локально-оптимальный план, то его нужно искать среди условно-стационарных точек задачи (1). Так как
– локально-оптимальный план, то его нужно искать среди условно-стационарных точек задачи (1). Так как  , то система (10) может быть записана в виде:
, то система (10) может быть записана в виде:
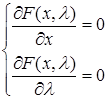 (10*)
(10*)
Таким образом, условно-стационарные точки как бы являются решением задачи на безусловный экстремум:
 .
.

 (1)
(1) , то есть правило справедливо для классической функции Лагранжа. Однако это было ошибкой. Покажем это на следующем примере.
, то есть правило справедливо для классической функции Лагранжа. Однако это было ошибкой. Покажем это на следующем примере. (здесь необязательно оптимальный) будем называть обыкновенным, если вектора
(здесь необязательно оптимальный) будем называть обыкновенным, если вектора (7)
(7) .
.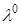 , что выполняется условие:
, что выполняется условие: (8)
(8) . Предположим противное, то есть
. Предположим противное, то есть  . Тогда из условия (5*) получаем
. Тогда из условия (5*) получаем , (9)
, (9) нулевые. Тогда (9) означает линейную зависимость векторов
нулевые. Тогда (9) означает линейную зависимость векторов  .
.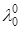 и переобозначим:
и переобозначим:  , тогда придём к условию (8).
, тогда придём к условию (8). такой, что
такой, что 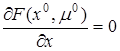 . Вычитая из этого равенства равенство (8), придём к
. Вычитая из этого равенства равенство (8), придём к  , причём не все коэффициенты
, причём не все коэффициенты  . Это означает линейную зависимость векторов (7) и снова противоречит обыкновенности
. Это означает линейную зависимость векторов (7) и снова противоречит обыкновенности  (10)
(10) (11)
(11) уравнений относительно
уравнений относительно 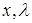 . Среди решений этих систем и только среди них нужно искать
. Среди решений этих систем и только среди них нужно искать  называется условно-стационарной точкой задачи (1),если она является решением системы (10).
называется условно-стационарной точкой задачи (1),если она является решением системы (10). , то система (10) может быть записана в виде:
, то система (10) может быть записана в виде: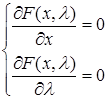 (10*)
(10*) .
.


