Рассмотрим задачу  (15)
(15)
 – выпуклая функция,
– выпуклая функция,  – выпуклое множество,
– выпуклое множество,  . Функцию
. Функцию 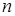 переменных, около некоторой точки
переменных, около некоторой точки  (в малой окрестности) можно разложить в ряд Тейлора
(в малой окрестности) можно разложить в ряд Тейлора
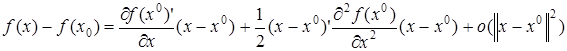 (16)
(16)
Разложение (16) справедливо лишь для  в малой окрестности точки
в малой окрестности точки  .
.
Теорема 3. Для того чтобы  был оптимальным планом задачи (15) необходимо и достаточно, чтобы
был оптимальным планом задачи (15) необходимо и достаточно, чтобы  (17). А в случае, когда
(17). А в случае, когда  , то (17) эквивалентно условию стационарности
, то (17) эквивалентно условию стационарности
 . (18)
. (18)
Доказательство. Необходимость. Пусть  – оптимальный план задачи (15). Возьмем произвольную точку
– оптимальный план задачи (15). Возьмем произвольную точку  и построим точку
и построим точку  . Если
. Если  достаточно мало, то точка
достаточно мало, то точка  лежит в сколь угодно малой окрестности
лежит в сколь угодно малой окрестности  . Запишем разложение:
. Запишем разложение:
 .
.
Так как левая часть равенства  , то неотрицательно и первое слагаемое справа. А так как
, то неотрицательно и первое слагаемое справа. А так как  , то приходим к (17).
, то приходим к (17).
Пусть теперь к тому же  – внутренняя точка. Построим вектора
– внутренняя точка. Построим вектора  . При достаточно малом
. При достаточно малом  . Подставляя его в (17):
. Подставляя его в (17):
 .
.
Так как  , то
, то  . Из этого неравенства следует (18).
. Из этого неравенства следует (18).
Если предположить  и положить
и положить  , то придем к противоречию.
, то придем к противоречию.
Достаточность. Пусть выполняется (17). Докажем, что  – оптимальный план задачи (15). Так как функция
– оптимальный план задачи (15). Так как функция  – гладкая и выпуклая, то для нее выполняется гладкий критерий выпуклости:
– гладкая и выпуклая, то для нее выполняется гладкий критерий выпуклости: 
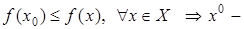 оптимальный план.
оптимальный план.
Ч.т.д.
Из этой теоремы и теоремы Куна-Таккера следует схема исследования гладкой основной задачи выпуклого программирования ( ,
,  ).
).
Пусть  оптимальный план такой задачи. Тогда по теореме Куна-Таккера для нее выполняется неравенство:
оптимальный план такой задачи. Тогда по теореме Куна-Таккера для нее выполняется неравенство:  . Если рассмотрим правую часть неравенства, то оно означает, что на множестве
. Если рассмотрим правую часть неравенства, то оно означает, что на множестве  (выпуклом) функция
(выпуклом) функция  достигает своего минимума в точке
достигает своего минимума в точке  , то есть оптимальный план основной задачи выпуклого программирования является оптимальным планом задачи
, то есть оптимальный план основной задачи выпуклого программирования является оптимальным планом задачи  (19). Афункция
(19). Афункция  является выпуклой и гладкой, то есть задача (19) такая же как и (15). В частности, если предположить, что
является выпуклой и гладкой, то есть задача (19) такая же как и (15). В частности, если предположить, что  , то для
, то для  должно выполняться неравенство
должно выполняться неравенство  . (20)
. (20)
Поэтому задачу нахождения оптимального плана основной задачи выпуклого программирования или задачу нахождения седловой точки можно свести к алгебраической задаче решения системы уравнений.
1) Сначала оптимальный план ищется на внутренности множества  , то есть предполагаем, что
, то есть предполагаем, что  . В силу вышесказанного и теоремы Куна-Таккера следует, что седловую точку надо искать среди решения системы уравнений
. В силу вышесказанного и теоремы Куна-Таккера следует, что седловую точку надо искать среди решения системы уравнений
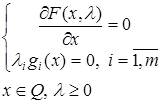 (21)
(21)
Первое уравнение следует из (20), а второе – из условия дополняющей не жесткости. Решение системы (21) относительно неизвестных  будем называть условно-стационарными точками.
будем называть условно-стационарными точками.
Ясно, что если  – седловая точка функции Лагранжа,
– седловая точка функции Лагранжа,  , то эта пара – условно-стационарная точка.
, то эта пара – условно-стационарная точка.
Система уравнений (21) относительно переменных  представляет собой систему из
представляет собой систему из  уравнений и
уравнений и  переменных.
переменных.
Пусть мы нашли все условно-стационарные точки. Тогда если  – одна из них, то подставляем ее в двойное неравенство и проверяем его справедливость. Если оно верно, то мы построили седловую точку и можно записать ответ:
– одна из них, то подставляем ее в двойное неравенство и проверяем его справедливость. Если оно верно, то мы построили седловую точку и можно записать ответ:  . Если же это неравенство неверно (нарушается хотя бы для одного
. Если же это неравенство неверно (нарушается хотя бы для одного  или хотя бы одного
или хотя бы одного  ), то
), то  не является оптимальным планом. Проверив все условно-стационарные точки поочередно, мы либо найдем оптимальный план задачи, либо докажем, что его нет на
не является оптимальным планом. Проверив все условно-стационарные точки поочередно, мы либо найдем оптимальный план задачи, либо докажем, что его нет на  .
.
2) Оптимальный план может находиться и на границе 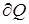 . Так как множество
. Так как множество  имеет простую структуру, то его граница простая, то есть состоит из некоторых частей плоскостей, ребер, угловых точек. Разбиваем
имеет простую структуру, то его граница простая, то есть состоит из некоторых частей плоскостей, ребер, угловых точек. Разбиваем 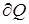 на отдельные элементы:
на отдельные элементы:
 , причем на каждом таком элементе либо одна, либо несколько переменных задачи фиксированы.
, причем на каждом таком элементе либо одна, либо несколько переменных задачи фиксированы.

 .
.
Перебирая поочередно все элементы границы, на каждом из них рассмотрим основную задачу выпуклого программирования, а так как там некоторые переменные фиксированы, то задача упрощается – имеет меньшее количество неизвестных, но она все равно относится к типу основных задач выпуклого программирования. Снова упрощенную задачу исследуем, как и на первом этапе, то есть строим систему, подобную (21), но более простую, находим условно-стационарные точки и каждую из них проверяем на седловую для исходной задачи.
Замечание. У словно-стационарную точку, найденную на границе, подставляем в двойное неравенство для функции Лагранжа исходной задачи, а не упрощенной.
Если мы построим седловую точку (докажем двойное неравенство), то процесс исследования прекращается и записывается ответ. Если же перебрав все элементы границы и все условно-стационарные точки, мы нигде не обнаружим седловой точки, то это означает, что у исходной основной задачи выпуклого программирования нет оптимального плана и на 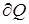 , а значит и вообще.
, а значит и вообще.

 (15)
(15) – выпуклая функция,
– выпуклая функция,  – выпуклое множество,
– выпуклое множество,  . Функцию
. Функцию 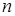 переменных, около некоторой точки
переменных, около некоторой точки  (в малой окрестности) можно разложить в ряд Тейлора
(в малой окрестности) можно разложить в ряд Тейлора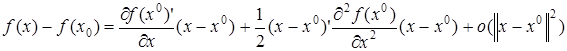 (16)
(16) в малой окрестности точки
в малой окрестности точки  (17). А в случае, когда
(17). А в случае, когда  , то (17) эквивалентно условию стационарности
, то (17) эквивалентно условию стационарности . (18)
. (18) и построим точку
и построим точку  . Если
. Если  достаточно мало, то точка
достаточно мало, то точка  лежит в сколь угодно малой окрестности
лежит в сколь угодно малой окрестности  .
. , то неотрицательно и первое слагаемое справа. А так как
, то неотрицательно и первое слагаемое справа. А так как  , то приходим к (17).
, то приходим к (17). . При достаточно малом
. При достаточно малом  . Подставляя его в (17):
. Подставляя его в (17): .
. , то
, то  . Из этого неравенства следует (18).
. Из этого неравенства следует (18). и положить
и положить  , то придем к противоречию.
, то придем к противоречию. – гладкая и выпуклая, то для нее выполняется гладкий критерий выпуклости:
– гладкая и выпуклая, то для нее выполняется гладкий критерий выпуклости: 
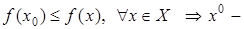 оптимальный план.
оптимальный план. ,
,  ).
). оптимальный план такой задачи. Тогда по теореме Куна-Таккера для нее выполняется неравенство:
оптимальный план такой задачи. Тогда по теореме Куна-Таккера для нее выполняется неравенство:  . Если рассмотрим правую часть неравенства, то оно означает, что на множестве
. Если рассмотрим правую часть неравенства, то оно означает, что на множестве  (выпуклом) функция
(выпуклом) функция  достигает своего минимума в точке
достигает своего минимума в точке  , то есть оптимальный план основной задачи выпуклого программирования является оптимальным планом задачи
, то есть оптимальный план основной задачи выпуклого программирования является оптимальным планом задачи  (19). Афункция
(19). Афункция  является выпуклой и гладкой, то есть задача (19) такая же как и (15). В частности, если предположить, что
является выпуклой и гладкой, то есть задача (19) такая же как и (15). В частности, если предположить, что  , то для
, то для  должно выполняться неравенство
должно выполняться неравенство  . (20)
. (20)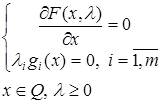 (21)
(21) будем называть условно-стационарными точками.
будем называть условно-стационарными точками. – седловая точка функции Лагранжа,
– седловая точка функции Лагранжа,  уравнений и
уравнений и  – одна из них, то подставляем ее в двойное неравенство и проверяем его справедливость. Если оно верно, то мы построили седловую точку и можно записать ответ:
– одна из них, то подставляем ее в двойное неравенство и проверяем его справедливость. Если оно верно, то мы построили седловую точку и можно записать ответ:  . Если же это неравенство неверно (нарушается хотя бы для одного
. Если же это неравенство неверно (нарушается хотя бы для одного  или хотя бы одного
или хотя бы одного  ), то
), то  не является оптимальным планом. Проверив все условно-стационарные точки поочередно, мы либо найдем оптимальный план задачи, либо докажем, что его нет на
не является оптимальным планом. Проверив все условно-стационарные точки поочередно, мы либо найдем оптимальный план задачи, либо докажем, что его нет на  .
.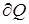 . Так как множество
. Так как множество  , причем на каждом таком элементе либо одна, либо несколько переменных задачи фиксированы.
, причем на каждом таком элементе либо одна, либо несколько переменных задачи фиксированы.
 .
.


