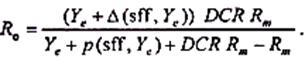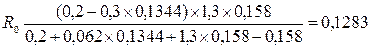Расчет текущей стоимости

Поступления	Размер, долл.	Фактор (20%, 5лет)	Текущая стоимость, долл.
Операционный доход	70000 х 2, 990612 = 209342, 8 + 700000 х 0, 4018776 = 281 314, 3
Выручка от продажи
Текущая стоимость денежного потока	490657, 1

 

Таким образом, инвестиции в размере 490 660 долл. (округленно) без привлечения кредита обеспечат инвестору 20%-ю конечную отдачу. Хотя текущая отдача равна

 

70000/490660= 0, 1427(14, 27%),

 

она увеличится до значения конечной отдачи в 20% вследствие увеличения стоимости недвижимости за прогнозный период.

2. Теперь определим обоснованную цену недвижимости, приобретаемой с привлечением кредита. Для решения используем традиционную технику в алгебраической форме.

Алгебраическое выражение для стоимости записывается в такой же трехэтапной логической последовательности:

 

V = I + II + МР,

 

где МР — текущий остаток основной суммы долга;

(pvaf Y_e, n)— фактор текущей стоимости единичного аннуитета при конечной отдаче на собственный капитал Y_eи сроке n;

NOI — чистый операционный доход;

DS — ежегодное обслуживание долга;

(pvfY_e, n) —фактор текущей стоимости единицы (реверсии);

RP — цена перепродажи недвижимости (реверсия);

OS — остаток долга в конце срока п.

Подставляем в это выражение исходные данные и значения факторов, определенные выше. Значения DS и OS рассчитываются исходя из известных условий кредита:

 

V= 2, 99 (70 000 - 47 404, 4) + 0, 4 (700 000 - 282 252, 4) + 300 000,

V = 534 660 долл. (округленно).

 

Рассчитанная обоснованная цена в 534 660 долл. выше, чем цена объекта, приобретаемого без заемных средств. Как было сказано раньше, инвестора интересуют прежде всего цена и рост собственного капитала. Инвестор готов заплатить большую сумму при положительном левередже, как это имеет место в данном случае (отдача на собственный капитал выше, чем ставки процента по кредиту), за возможность значительно увеличить конечную отдачу на собственные средства и уменьшить собственные капиталовложения.

Алгебраическая форма традиционной техники удобна, когда величины текущей задолженности и (или) перепродажи определяются в долях (процентах) от первоначальной цены недвижимости. Запишем общее выражение в алгебраической форме, когда вместо величины кредита известен коэффициент ипотечной задолженности т, астоимость определена в долях Δ от текущей цены V.

 

V = (pvaf)(N0I-mVDS₁) + [(pvf)(l±Δ)V-mVOS₁)] + mV,

 

где DS₁ — обслуживание долга при единичном кредите, или ипотечная постоянная;

OS₁ — невыплаченная доля кредита к концу прогнозного периода, или остаток долга при единичном кредите;

Δ — доля увеличения или уменьшения стоимости недвижимости.

3. Допустим, что вместо величины кредита дан коэффициент ипотечной задолженности т = 60%, а вместо цены перепродажи — увеличение стоимости за период владения на 25%.

Подставляемчисленные значения:

V =2, 99(70000 — 0, 6V 0, 158)+ 0, 4 (1, 25 V—0, 6V 0, 938) + 0, 6 V,

V = 512 236, 91=512 237 долл.

 

4. Определим с помощью традиционной техники цену недвижимости с существующей закладной. Предположим, что недвижимость в текущем состоянии обременена закладной в обеспечение ипотечного кредита, полученного семь лет назад в размере 300 000 долл. на срок в двадцать лет с ежемесячными платежами 15% годовых. Остальные условия —из базового примера.

Текущий остаток долга составляет

МР = 270 519, 95 долл. (из условия кредита).

 

Остаток долга на момент реверсии:

 

OS= 166 052, 17 долл. (через 7+ 5 = 12 лет).

 

Подставляем значения:

V = 2, 99 (70 000 - 47 404, 4) + 0, 4 (700 000 - 166 052, 17) + 270 519, 95,

V =551 660 долл.

 

5. Определить ставку конечной отдачи на собственный капитал при известных параметрах проекта к текущей цене недвижимости. Такая задача может возникнуть, например, когда оценщик пытается определить требования инвесторов на конкретном рынке, опираясь на недавно проданные аналоги с известными инвестиционными параметрами.

При использовании алгебраической формы для решения этой задачи следует определить факторы (pvaf) и (pvf) при различных ставках отдачи и подставлять их в равенство с известной текущей ценой SP до тех пор, пока это равенство не превратится в тождество.

Задача решается методом приближения и гораздо быстрее с использованием финансового калькулятора, так как конечная отдача на собственный капитал при известной текущей величине собственного капитала равна внутренней норме прибыли IRR для собственного капитала и соответствующего денежного потока.

Воспользуемся данными из предыдущего примера.

Текущая стоимость собственного капитала: 551660-270520 = 281 140 долл.

Доход на собственный капитал: 70 000 - 47 404, 4 = 22 595, 6 долл./год.

Выручка от продажи: 700 000 - 166 052 = 533 948 долл.

Результат расчета: Y_e= IRR 20%.

Получаем значение Y_e, при котором стоимость инвестиций в собственный капитал в размере 281 140 долл. соответствует спрогнозированному денежному потоку.

Традиционная техника ипотечно-инвестиционного анализа позволяет сделать определенные выводы относительно влияния величины прогнозного периода на результаты оценки. Важным фактором, ограничивающим с точки зрения инвесторов период владения, является уменьшение со временем амортизационных (активы) и процентных вычетов из прибыли для налогообложения. Кроме того, возможно появление более предпочтительных вариантов инвестирования (внешние факторы). С другой стороны, постепенно уменьшается текущее значение коэффициента ипотечной задолженности, что приводит к падению эффективности финансового левереджа. Анализ с помощью традиционной техники вариантов с различными сроками владения показывает очевидное влияние прогнозного периода на величину оцениваемой стоимости. При этом зависимость такова, что при увеличении прогнозируемого срока владения величина оцениваемой стоимости уменьшается при отсутствии изменения стоимости за прогнозные периоды.

Техника Эллвуда. Она используется в инвестиционно-ипотечном анализе и дает те же результаты, что и традиционная техника, так как основывается на том же наборе исходных данных и представлениях о взаимоотношении интересов собственного и заемного капиталов за период развития инвестиционного проекта. Отлично техники Эллвуда заключается в том, что он позволяет анализировать собственность относительно ее цены на основе коэффициентов доходности долевых показателей в структуре инвестиций, изменения стоимости всего капитала и достаточно наглядно показывает механизм изменения собственного капитала за инвестиционный период.

Общий вид формулыЭллвуда:

 

R_о =[Y-mC + Δ (sff, Y_e)]/(l + Δ _na),

 

где R₀ — общий коэффициент капитализации;

С — ипотечный коэффициент Эллвуда;

Δ — долевое изменение стоимости собственности;

(sff, Y_e) — фактор фонда возмещения по ставке отдачи на собственный капитал;

Δ _n — долевое изменение дохода за прогнозный период;

а —коэффициент стабилизации.

Ипотечный коэффициент Эллвуда:

 

С = Y_e+ p(sff, Y_e)-R_m ,

 

где р — доля текущего остатка кредита, самортизированного за прогнозный период,

R_m — ипотечная постоянная относительно текущего остатка долга.

Выражение 1/(1 + Δ _n а) в уравнении — стабилизирующий множитель и используется, когда доход не постоянный, а регулярно изменяется. Обычно задается закон изменения дохода (например, линейный, экспоненциальный, по фактору фонда накопления), в соответствии с которым определяется коэффициент стабилизации а по заранее рассчитанным таблицам. Стоимость определяется делением дохода за год, предшествующий дате оценки, на коэффициент капитализации с учетом стабилизации дохода. В дальнейшем будем рассматривать технику Эллвуда только для постоянных доходов.

Запишем выражение Эллвуда без учета изменения стоимости недвижимости и при постоянном доходе:

 

R = Y_e - т [Y_e + р (sff, Y_e) - R_m ].

 

Это выражение называется базовым коэффициентом капитализации, который равен ставке конечной отдачи на собственный капитал с корректировкой на условия финансирования и амортизации.

Рассмотрим структуру общего коэффициента капитализации в формуле Эллвуда без учета изменений стоимости собственности, для чего используем технику инвестиционной группы для ставок отдачи. Эта техника взвешивает ставки отдачи на собственный и заемный капитал в соответствующих долях всего инвестированного капитала:

 

Y₀=mY_m +(1-m)Y_e.

 

Для того чтобы это выражение стало эквивалентным базовому коэффициенту r, необходимо учесть еще два фактора. Первый заключается в том, что инвестор должен периодически отчислять из своего дохода на амортизацию кредита, уменьшая собственный капитал. Следовательно, необходимо скорректировать величину Y₀ в предыдущем выражении путем прибавления периодически выплачиваемойдоли всего капитала под процент, равный ставке процента по кредиту. Выражение этой корректировки представляет собой долю заемного капитала т, умноженную на фактор фонда возмещения по ставке процента (sff, Y_m). Величина (sff,)Y_m) равна разности между ипотечной постоянной и ставкой процента, т. е. R_m -Y_m. Таким образом, с учетом этой поправки:

 

Y₀ = mY_m + (1 -m)Y_e + m(R_m -Y_m).

 

Второй корректирующий член должен учесть тот факт, что собственный капитал инвестора в результате реверсии увеличится на величину части кредита, самортизированной за период владения. Чтобы определить эту корректировку, нужно умножить самортизированную сумму в долях от всего первоначального капитала на фактор фонда возмещения по ставке конечной отдачи на собственный капитал (реализация в собственный капитал происходит в конце периода владения). Следовательно, второй корректирующий член имеет вид: mp(sff, Y_m), причем со знаком " минус", так как эта поправка увеличивает стоимость.

Таким образом:

 

Y₀ = mY_m+(1-m)Y_e+m(R_m -Y_m)-mp(sff, Y_e),

 

и после объединения подобных членов и замены Y₀ на r(не учитываем изменение стоимости собственности):

 

r = Y₀ -m[Y_e +(p(sff)-R_m)].

 

Таким образом, получаем базовый коэффициент капитализации выражения Эллвуда. Последовательный переход от техники инвестиционной группы через учет необходимых корректировок к выражению Эллвуда показывает, что это выражение действительно отражает все элементы трансформации собственных и заемных средств, объединенных в инвестированном капитале, в частности финансовый левередж, амортизацию ипотечного кредита и прирост собственного капитала в результате амортизации кредита.

ПРИМЕРЫ

1. Оценить свободную от задолженности доходную недвижимость, которая в течение пятилетнего срока владения приносит чистый ежегодный доход 70 000 долл. К концу этого срока стоимость недвижимости увеличится на 30%. Инвестор требует 20%-ю конечную отдачу на собственный капитал.

В этом случае формула будет иметь следующий вид:

 

R = Y_e + Δ (sff, Y_e),

 

так как m = 0 по условию задачи.

(sff, Y_e 5 лет) = 0, 1344.

Подставим значения:

 

R = 0, 2 -0, 3 х 0, 1344 = 0, 1597;

V=NOI/R = 70 000/0, 1597 = 438 360 долл.

 

2. Та же недвижимость приобретается с привлечением ипотечного кредита в размере 60% стоимости недвижимости на двадцать лет с ежемесячным платежом 15% годовых. Определить стоимость недвижимости.

Выражение Эллвуда для общей ставки капитализации:

 

R₀ = Y_e-m[Y_e + p(sff, Y_e)-R_m]+ Δ (sff, Y_e).

 

После подстановки значений:

 

R₀= 0, 2-0, 6(0, 2+ 0, 0594x0, 1344-0, 158)-0, 3x0, 1344 = 0, 1297;

V = NOI /R_o= 70 000/0, 1297 = 539 707 долл.

 

Технику Эллвуда можно использовать, если долг и увеличение стоимости недвижимости заданы в денежном выражении. В этом случае коэффициенты и долевые параметры выражаются через стоимость V.

3. Недвижимость (предыдущий пример) приобретается с привлечением кредита в размере 300 000 долл. Ожидается увеличение стоимости недвижимости за пять лет на 160 000 долл. Какова обоснованная максимальная цена недвижимости?

Напишем уравнение Эллвуда, подставив известные и рассчитанные величины и выразив соответствующие параметры через стоимость:

 

V =532 -195 долл.

 

В случае оценки недвижимости с существующей закладной необходимо учесть, что величины р, R_m и т в формуле Эллвуда представляют собой погашенную за прогнозный период часть долга относительно текущего остатка, ипотечную постоянную, рассчитанную на основе текущего остатка кредита, и текущий коэффициент ипотечной задолженности соответственно.

4. Определим цену недвижимости с существующей закладной по ипотечному кредиту, выданному семь лет назад в размере 60% стоимости на двадцать лет под 15% годовых с ежемесячными платежами без учета изменения стоимости.

 

R_о = r = Y_e - M [Y_e + p(sff, Y_e)- R_m].

 

Определим текущие значения m, R_m и р:

 

m = 0, 5383; R_m=0, 1761; p = 0, 1957.

r = 0, 2 - 0, 53883 (0, 2 + 0, 1957 х 0, 1344-0, 1761) = 0, 173;

V= 70 000/0, 173 = 404 680 долл.

 

Уравнение Эллвуда, выраженное через коэффициент покрытия долга. Финансирование проектов, связанных со значительными рисками относительно получения стабильных доходов, может изменить ориентацию кредиторов относительно критерия, определяющего размер заемных средств. Кредитор полагает, что в этой ситуации размер кредита целесообразнее определять не на ценовой основе, а на базе отношения годового чистого дохода инвестора к годовым платежам по заемному обязательству, т. е. кредитор требует гарантий, что величина этого отношения (естественно, больше единицы) не будет меньше некоторого минимального определенного кредитором значения. Это отношение называют коэффициентом покрытия долга: DCR = NOI/DS.

В этом случае коэффициент ипотечной задолженности в уравнении Эллвуда следует выразить через коэффициент покрытия долга DCR:

 

DCR = NOI/DS = RV/(R_mY_m,)=R/(R_mm), или m = R/(DCRR_m).

 

После подстановки этого выражения вместо m получаем уравнение Эллвуда, выраженное через коэффициент покрытия долга:

 

 

ПРИМЕР

5. Оценить доходную недвижимость, приносящую чистый ежегодный доход 70 000 долл., срок владения 5 лет. Предполагается, что по истечении этого срока стоимость недвижимости увеличится на 30%. Недвижимость приобретается с привлечением ипотечного кредита под 15% годовых, с ежемесячными платежами, 20-летним сроком и коэффициентом покрытия долга, равным 1, 3. Инвестор требует 20%-ю конечную отдачу на собственный капитал.

Подставляем значения и определяем общий коэффициент капитализации:

 

SP = 70 000/0, 1283 = 545 800 долл.

 

7.4. Влияние ипотечного кредита на соотношение " цена — стоимость"

Выше отмечалось, что основной интерес инвестора заключается в увеличении собственного капитала в результате реализации инвестиционного проекта. Собственник должен оптимизировать структуру капитала, взвешивая все издержки, риск и стоимость обслуживания долга и сопоставляя их с будущей эффективностью использования собственных и заемных средств. Инвестор считает, что успешным является проект с использованием дешевого кредита с желаемым коэффициентом задолженности, длительным сроком амортизации и нормой отдачи на собственный капитал, отвечающей его требованиям. За реализацию этих условии инвестор готов заплатить цену большую, чем рыночная стоимость недвижимости. Таким образом, конкретные условия финансирования влияют на величину денежных средств, уплаченных за недвижимость в результате конкретной сделки купли-продажи, но не на ее стоимость. Условия финансирования не влияют на физическую сущность собственности и арендные платежи. Для перевода цены в стоимость (иногда используется термин " денежный эквивалент рыночной стоимости") оценщик должен хорошо ориентироваться в типичных предпочтениях кредиторов и инвесторов.

В примерах, иллюстрировавших использование техники ипотечпо-инвестиционного анализа, определялась обоснованная цена, или оценочная стоимость, именно вследствие того, что исходными данными служили конкретные (частные) условия финансирования. Для того чтобы определить стоимость недвижимости, которая в соответствии с основным смыслом инвестиционно-ипотечного анализа является суммой текущих рыночных интересов финансовых составляющих, нужно определить рыночную стоимость долгового обязательства и сложить ее с собственным капиталом (платежом) покупателя.

Рассмотрим несколько примеров, в которых оценщик рассматривает аналоги объекта оценки с известными ценой и условиями финансирования.

ПРИМЕРЫ

1. Недвижимость, приносящая 60 000 долл. ежегодного чистого дохода, приобретена за 560 000 долл. с привлечением ипотечного кредита в размере 400 000 долл., предоставленного на 20 лет под 10% годовых с ежемесячными платежами. Наиболее вероятное значение годовой процентной ставки для ипотечных кредитов па данном рынке составляет около 15%. Привести цену, уплаченную за недвижимость, к рыночному значению можно, или скорректировав величину кредита соответственно с рыночной ставкой процента, или определив непосредственно величину надбавки к стоимости.

ВАРИАНТ 1. Ежемесячные платежи по 10%-му кредиту — 3 860, 09 долл.

Величина кредита при указанных ежемесячных платежах и 15% годовых 293 144 долл.

Таким образом, цена, приведенная к стоимости:

160000долл. (собственный капитал)+ 293 144долл.=453 144 долл.