МИНОР И АЛГЕБРАИЧЕСКОЕ ДОПОЛНЕНИЕ
Вопросы
1. Образовать все подмножества множества {1, 2, 3}. 2. Как выражается количество различных подмножеств множества, состоящего из 3. Пояснить с помощью графика, из каких элементов состоит множество
1.1.2. Объединение и пересечение множеств
Объединением (суммой) множеств

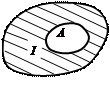
Рис.1.2 Объединение множеств обозначается через Подобные геометрические интерпретации называются диаграммами Эйлера-Венна.[2] Аналогично определяется объединение
Например, 1) 2) Символ импликации Пересечением (произведением) множеств Обозначается пересечение через Аналогично определяется пересечение
Например, 1) 2) Относительно введенных действий над множествами справедливы следующие свойства: 1) коммутативность (переместительный закон): 2) ассоциативность (сочетательный закон): 3) идемпотентность[3] (тождественность): 4) дистрибутивность (распределительный закон): В алгебре множеств для доказательства равенства вида
откуда следует, что Если в (1.2.6) повернуть знаки импликации в противоположную строну, то получаются снова верные соотношения, из которых следует, что
Вопросы
1. Как проиллюстрировать равенство (1.2.5) с помощью диаграммы Эйлера-Венна? 2. Чему равно 3. В каких отношениях находятся множества
1.1.3. Разность множеств. Дополнение множества
Разностью множеств
  Обозначается разность Обозначается разность  , ее геометрическая иллюстрация приведена на рис. 1.3, а. , ее геометрическая иллюстрация приведена на рис. 1.3, а.
a б Рис.1.3 В этом определении существенен порядок, в котором следуют множества:
Например, Разность
Вопросы
1. Чему равно 2. Как выразить через дополнения
Полученные в соответствии с последним вопросом равенства называются формулами де Моргана. [4] Для произвольного числа множеств они имеют вид
Множество элементов
1.1.4. Декартово произведение множеств
Любым двум объектам Декартовым произведением множеств А и В называется множество всех упорядоченных пар элементов Обозначается декартово произведение через
Декартово произведение n множеств определяется аналогично:
Напомним обозначения:
Вопросы
При каком условии: а) б)
1.1.5. Мощность множества
Понятие мощности множества связано с запасом элементов в этом множестве. Два множества имеют (по определению) одинаковую мощность, если между их элементами можно установить взаимно однозначное соответствие. Такие множества называются эквивалентными (равномощными). Два конечных множества эквивалентны тогда и только тогда, когда они состоят из одинакового числа элементов. Приведем примеры эквивалентных бесконечных множеств: 1) множество натуральных чисел
2) в прямоугольном треугольнике множество точек гипотенузы эквивалентно множеству точек любого катета (рис. 1.5, а); 3) множества точек на двух любых окружностях являются эквивалентными (рис. 1.5, б). Множество, эквивалентное множеству натуральных чисел, называется счетным.
Приведем примеры счетных множеств:
Теорема 1. Объединение конечного или счетного множества счетных множеств является счетным множеством. Для доказательства рассмотрим счетную совокупность
где
……………………………. Тогда объединение
При этом никакие элементы Если некоторые из множеств Теорема 2. Множество рациональных чисел является счетным множеством. Для доказательства введем счетные множества
Очевидно, что множество
есть множество положительных рациональных чисел. Согласно теореме 1 оно является счетным. Точно так же счетным будет и множество
тоже оказывается счетным множеством в силу теоремы 1, что и требовалось доказать. Теорема 3. Множество действительных чисел на отрезке [0, 1] имеет мощность, большую мощности счетного множества. Для доказательства теоремы наряду с множеством
рассмотрим множество десятичных дробей
Среди элементов множества 1) между множествами 2) если две дроби из При этом множество Предположим, что множество
Образуем новую бесконечную десятичную дробь
выбрав
Очевидно, что, с одной стороны, Всякое множество, эквивалентное множеству действительных чисел отрезка [0, 1], имеет (по определению) мощность континуума. [6] Вопросы
1. Какова мощность множества всех корней квадратных уравнений с рациональными коэффициентами? 2. Всякое число, являющееся корнем многочлена с рациональными коэффициентами, называется алгебраическим. Какова мощность множества алгебраических чисел? 3. Какова мощность множества точек отрезка [а, b]? 4. На плоскости задано некоторое бесконечное множество непересекающихся окружностей. Может ли это множество быть несчетным? 5. Какова мощность множества точек всей числовой оси?
Из ответа на последний вопрос ясно, что множество всех действительных чисел имеет мощность континуума. Можно доказать, что множества всех точек на плоскости или в пространстве имеют такую же мощность. Может возникнуть вопрос, существуют ли множества высших мощностей. Положительный ответ здесь дает следующая теорема Кантора [7]: множество, элементами которого являются все подмножества некоторого множества А, имеет мощность, большую мощности множества В связи с изложенным может возникнуть и другой вопрос: существуют ли множества промежуточной мощности между мощностью счетного множества и континуума (так называемая континуум - гипотеза). Недавно (1964 г.) американским математиком Коэном было установлено, что указанное предложение никакими принятыми в математике способами невозможно ни доказать, ни опровергнуть. Таким образом, можно полагать, что континуум - гипотеза, по существу, является аксиомой: приняв ее или отвергнув, мы не вступаем в противоречие с другими положениями математики.
ГЛАВА ВТОРАЯ ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ 2.1. ПОНЯТИЕ О МАТРИЦЕ
При решении многих математических и прикладных задач возникает необходимость рассматривать совокупность чисел, расположенных в виде таблиц, что позволяет значительно упростить форму записи. Например, рассмотрим систему трех уравнений с тремя неизвестными:
Информацию о ней можно закодировать с помощью таблицы
а информацию о коэффициентах системы — с помощью другой таблицы:
С помощью таблиц можно задавать и функции. Так, функцию
можно задать и по-другому:
В связи с изложенным введем новое понятие. Прямоугольной
содержащая Числа В литературе используются и другие, более краткие обозначения матрицы. Например,
Матрица (1.1) называется квадратной матрицей n-го порядка, если Квадратная матрица порядка n называется диагональной, если
и иногда обозначается Диагональная матрица порядка п называется единичной матрицей, если все ее элементы равны единице
Используется также обозначение
где
Матрица произвольной размерности, все элементы которой равны нулю, называется нулевой матрицей. Обозначается она через
Две
2.2. ОПРЕДЕЛИТЕЛИ ВТОРОГО И ТРЕТЬЕГО ПОРЯДКОВ
При решении многих математических задач возникает необходимость в сопоставлении квадратной матрице некоторого числа, называемого определителем. В данном курсе отдается предпочтение такому порядку изложения теории, когда понятие определителя вводится формально, затем изучаются свойства определителей и, наконец, устанавливается их связь с решением конкретных задач (в частности, с решением систем линейных уравнений). Рассмотрим квадратную матрицу второго порядка:
Определителем (детерминантом)[9] второго порядка матрицы (2.2.1) называется число
Он обозначается следующим образом:
Часто определитель обозначают одной буквой Для квадратной матрицы третьего порядка определитель вводится с помощью формулы
которая легко записывается с помощью правила треугольников:
Например,
2.3. ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
При доказательстве свойств определителей будем рассматривать ради краткости в основном определители второго порядка. Доказательство тех же свойств для определителей третьего порядка рекомендуем провести самостоятельно. С в о й с т в о 1. При транспонировании, т. е. при замене в определителе строк столбцами (с теми же номерами) величина определителя не изменяется:
Вычисляя определители, стоящие в обеих частях (2.3.1), получаем верное равенство
Заметим, что свойство 1 выражает равноправие строк и столбцов определителя, состоящее в том, что любое свойство, справедливое для строк, будет верно и для столбцов. С в о й с т в о 2. Если поменять местами две строки или два столбца определителя, то определитель изменит свой знак:
Доказывается свойство 2 непосредственным вычислением определителей, входящих в обе части равенства (2.3.2). С в о й с т в о 3. Определитель с двумя одинаковыми строками (столбцами) равен нулю. Это свойство является следствием свойства 2. Для доказательства в определителе С в о й с т в о 4. Общий множитель всех элементов строки (столбца) определителя можно выносить за знак определителя
Действительно, в результате вычислений получаем очевидное равенство
С в о й с т в о 5. Определитель с двумя пропорциональными строками (столбцами) равен нулю.
Для доказательства достаточно вынести, согласно свойству 4, за знак определителя множитель k. Тогда получим определитель с двумя одинаковыми строками, который равен нулю (свойство 3). С в о й с т в о 6. Имеет место формула
Доказательство выполняется очень просто:
С в о й с т в о 7. Определитель не изменится, если ко всем элементам некоторой его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число:
Для доказательства используем свойства 6 и 5:
В качестве упражнения вычислите определители третьего порядка a) а затем «организуйте» в каждом из них строку или столбец, содержащий только один ненулевой элемент.
МИНОР И АЛГЕБРАИЧЕСКОЕ ДОПОЛНЕНИЕ
Рассмотрим определитель n -ного порядка. Минором Алгебраическим дополнением
Например, минор для элемента
будет иметьвид
а алгебраическое дополнение равно
Нетрудно видеть, что знаки, которые следует ставить перед соответствующими минорами при вычислении алгебраических дополнений, чередуются в шахматном порядке:
В качестве упражнения выпишите алгебраические дополнения для элементов
Если рассматривается прямоугольная матрица, то понятие минора вводится по-иному. Выберем в Например, для матрицы
можно образовать миноры третьего, второго и первого порядков (определитель первого порядка считается равным своему элементу). Вот некоторые из них:
|

 элементов?
элементов? .
. и
и  называется множество, образованное из всех тех элементов, которые входят хотя бы в одно из множеств
называется множество, образованное из всех тех элементов, которые входят хотя бы в одно из множеств 
 B A
B A  B
B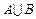 ; геометрическая иллюстрация этого понятия дана на рис. 1.2, а.
; геометрическая иллюстрация этого понятия дана на рис. 1.2, а. или
или  или
или  .
. ,
,  ,
, 

 ;
; ,
,  ,
, 

 , геометрическая иллюстрация приведена на рис. 1.2, б. Чтобы не путать знаки
, геометрическая иллюстрация приведена на рис. 1.2, б. Чтобы не путать знаки  (от «Union» — союз), а второй — как трансформированную букву П («пи»), которой означают произведение.
(от «Union» — союз), а второй — как трансформированную букву П («пи»), которой означают произведение.
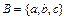 ,
, 
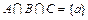 ;
;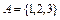 ,
,  ,
, 
 .
. ,
,  ; (1.2.1)
; (1.2.1) ,
, 
 ; (1.2.2)
; (1.2.2) ,
,  ; (1.2.3)
; (1.2.3) , (1.2.4)
, (1.2.4) . (1.2.5)
. (1.2.5) =
=  (
( и
и  . В качестве примера приведем схему доказательства равенства (1.2.5)
. В качестве примера приведем схему доказательства равенства (1.2.5)
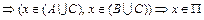 , (1.2.6)
, (1.2.6) ,
, 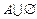 ,
,  ,
,  ?
?

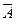

 .
. ,
, 
 ,
,  .
. называется дополнением множества
называется дополнением множества  (
(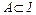 ). Дополнение обозначается через
). Дополнение обозначается через  (или
(или  ). Его геометрический смысл ясен из рис. 1.3, б.
). Его геометрический смысл ясен из рис. 1.3, б. ,
,  ,
, 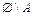 ,
,  ,
, 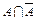 ,
,  ,
,  ,
, 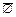 ?
? ,
,  ?
? ,
, 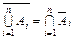 . (1.3.1)
. (1.3.1) и заданы два особых элемента
и заданы два особых элемента  и
и  и
и  можно сопоставить их упорядоченную пару
можно сопоставить их упорядоченную пару  . Этот прием лежит в основе определения декартова произведения множеств.
. Этот прием лежит в основе определения декартова произведения множеств. ,
,  .
. . Его геометрическая интерпретация приведена на рис. 1.4, где показаны следующие множества:
. Его геометрическая интерпретация приведена на рис. 1.4, где показаны следующие множества:
 ;
;
 .
.
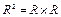 ,
,  ,...,
,...,  .
. ,
, ?
? эквивалентно своему подмножеству
эквивалентно своему подмножеству  , в которое входят все четные положительные числа, так как
, в которое входят все четные положительные числа, так как

 ;
;  ;
;  ,
,  .
. непересекающихся счетных множеств, т. е.
непересекающихся счетных множеств, т. е. , (1.5.1)
, (1.5.1)




 ;
;

 будет состоять из элементов, которые можно выписать в одну строку (и, следовательно, пронумеровать), «снимая» элементы послойно, как показано стрелками на схеме:
будет состоять из элементов, которые можно выписать в одну строку (и, следовательно, пронумеровать), «снимая» элементы послойно, как показано стрелками на схеме: (1.5.2)
(1.5.2) упущены не будут, и теорема при условии (1.5.1) доказана.
упущены не будут, и теорема при условии (1.5.1) доказана. имеют непустые пересечения друг с другом или рассматривается конечная совокупность множеств
имеют непустые пересечения друг с другом или рассматривается конечная совокупность множеств 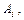 то доказательство изменяется несущественно: в строке (1.5.2) некоторые элементы нужно исключить, а оставшиеся элементы образуют счетное множество (можно, например, оставить все элементы множества
то доказательство изменяется несущественно: в строке (1.5.2) некоторые элементы нужно исключить, а оставшиеся элементы образуют счетное множество (можно, например, оставить все элементы множества  ;
; 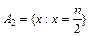 ;
;  ;...
;... 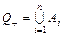 ,
, 
 — отрицательных рациональных чисел. Множество всех рациональных чисел
— отрицательных рациональных чисел. Множество всех рациональных чисел

 ,
,  .
. можно установить взаимно однозначное соответствие, т. е.
можно установить взаимно однозначное соответствие, т. е.  .
. ,
, ,
,  ,
, 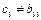 ,.... (1.5.3)
,.... (1.5.3) , т. е.
, т. е.  . С другой стороны, в силу (1.5.3)
. С другой стороны, в силу (1.5.3)  . Полученное противоречие убеждает нас в том, что множество
. Полученное противоречие убеждает нас в том, что множество 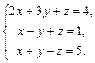
 ,
, .
. .
. матрицей называется таблица чисел
матрицей называется таблица чисел , (2.1.1)
, (2.1.1) строк и
строк и 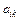 называются элементами матрицы. Первый индекс i указывает номер строки, в которой расположен элемент, а второй индекс k — номер столбца. Элементы
называются элементами матрицы. Первый индекс i указывает номер строки, в которой расположен элемент, а второй индекс k — номер столбца. Элементы  при i=const образуют i-тую строку матрицы, а при k = const — столбец с номером k.
при i=const образуют i-тую строку матрицы, а при k = const — столбец с номером k. ,
,  ,
,  ,
, 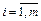 ,
,  .
. .
. при
при  . Она выглядит следующим образом:
. Она выглядит следующим образом:
 .
. :
: .
. ,
, — символ Кронекера[8]
— символ Кронекера[8]

 матрица называется матрицей-столбцом (вектор-столбцом):
матрица называется матрицей-столбцом (вектор-столбцом): .
. матрица называется матрицей-строкой (вектор-строкой):
матрица называется матрицей-строкой (вектор-строкой):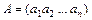 .
. и
и  называются равными тогда и только тогда, когда
называются равными тогда и только тогда, когда  при всех
при всех  и при всех
и при всех  . Равенство может рассматриваться только для матриц одной и той же структуры
. Равенство может рассматриваться только для матриц одной и той же структуры 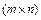 .
. . (2.2.1)
. (2.2.1) . (2.2.2)
. (2.2.2) .
.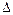 .
. , (2.2.3)
, (2.2.3)
 (2.2.4)
(2.2.4) .
. . (2.3.1)
. (2.3.1) .
. . (2.3.2)
. (2.3.2) с двумя одинаковыми строками поменяем эти строки местами. От этого он, естественно, не изменится. Однако согласно свойству 2 знак его должен измениться на противоположный:
с двумя одинаковыми строками поменяем эти строки местами. От этого он, естественно, не изменится. Однако согласно свойству 2 знак его должен измениться на противоположный:  . Отсюда следует, что
. Отсюда следует, что  .
.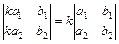 .
.

 .
. .
.

 б)
б)  в)
в) 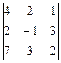 ,
, элемента
элемента  определителя n -ного порядка
определителя n -ного порядка  элемента
элемента  , умноженный на
, умноженный на  :
: .
. в определителе
в определителе
 ,
, .
.
 в определителе
в определителе .
. матрице какие-либо k строк и k столбцов
матрице какие-либо k строк и k столбцов  Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k- тогопорядка. Любой из таких определителей называется минором k- того порядка для данной матрицы.
Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k- тогопорядка. Любой из таких определителей называется минором k- того порядка для данной матрицы.
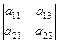 ,
, 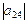 .
.


