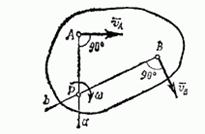
Связь между координатным и естественным способами задания движения точки
-- определить траекторию точки, исключив время из уравнений (3) -- найти закон движения точки по траектории (воспользоваться выражением для дифференциала дуги) После интегрирования получим закон движения точки по заданной траектории:
6.
7. Поступательным называется такое движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельной своему начальному направлению. Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во все время движения неподвижными Промежуток времени, в течение которого тело совершает один полный оборот вокруг оси, — период вращения. Величина, обратная периоду, — частота вращения. Проходящая через неподвижные точки А и В прямая АВ называется осью вращения. Угловую скорость тела можно изобразить в виде вектора ω =
При равномерном вращении абсолютно твердого тела углы поворота тела за любые равные промежутки времени одинаковы, тангенциальные ускорения у различных точек тела отсутствуют, а нормальное ускорение точки тела зависит от ее расстояния до оси вращения: Угловое ускорение характеризует изменение с течением времени угловой скорости тела.
Направление ε совпадает с направлением ω, когда тело вращается ускоренно и, противоположно ω при замедленном вращении
8.
9. 10.
Так же как при сложном движении точки нередко и движение тела можно рассматривать как сумму нескольких движений. Например, состоящее из двух поступательных движений или поступательного движения и вращения в округ оси. Часто встречаются движения, состоящие из двух вращений вокруг осей или поступательного движения и вращения вокруг точки. Исследование движения точек принадлежащих телу, совершающему сложное движение, можно проводить методами, изложенными выше и никаких особых трудностей не вызывает. Но анализ сложного движения тела, состоящего из нескольких вращений, обнаруживает некоторые особенности, которые следует рассмотреть специально. 11.
12. Сложение ускорений по параллелограму
13.
14. Эта задача заключается в том, что по заданным силам, приложенным к движущейся материальной точке, массе этой точки и начальным условиям ее движения (начальному положению и начальной скорости), требуется определить движение этой точки. Для решения этой задачи необходимо: 1) установить, какие силы действуют на материальную точку; 2) составить дифференциальные уравнения движения точки 3) проинтегрировать эти уравнения; 4) определить по начальным условиям движения произвольные постоянные, которые войдут в интегралы этих уравнений.
15.
16. Для его понимания нам потребуется ввести понятие системы отсчета, или координат. Как известно, положение движущегося тела в каждый момент времени определяется по отношению к некоторому другому телу, которое называется системой отсчета. С этим телом связана соответствующая система координат, например, привычная нам декартова система. На плоскости движение тела или материальной точки определяется двумя координатами: абсциссой х, показывающей расстояние точки от начала координат по горизонтальной оси, и ординатой у, измеряющей расстояние точки от начала координат по вертикальной оси. В пространстве к этим координатам добавляется третья координата z. Среди систем отсчета особо выделяют инерциальные системы, которые находятся друг относительно друга либо в покое, либо в равномерном и прямолинейном движении. Особая роль инерциальных систем заключается в том, что для них выполняется принцип относительности.
В таких системах законы движения тел выражаются той же самой математической формой, или, как принято говорить в науке, они являются ковариантными. Действительно, два разных наблюдателя, находящихся в инерциальных системах, не заметят в них никаких изменений.
17.
Следствие: если система консервативна, т.е. все силы потанциальны (Апотан.=-П) Т1-Т0=-(П1-П0) Т1+П1=Т0+П0=Е
18.
19.
20.
21.
При вращательном движении тела кинетическая энергия равняется половине произведения момента инерции тела относительно оси вращения и квадрата его угловой скорости. Мерой инертности тела при вращательном движении является момент инерции.
22.
23.
24.
25.
26.
27.
28.
|



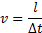

 — формула связи между линейной и угловой скоростью.
— формула связи между линейной и угловой скоростью.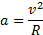
 , модуль которого равен |
, модуль которого равен | 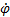 Таким образом, числовое значение угловой скорости тела в данный момент времени равно первой производной от угла поворота по времени. Знак ω определяет направление вращения тела.
Таким образом, числовое значение угловой скорости тела в данный момент времени равно первой производной от угла поворота по времени. Знак ω определяет направление вращения тела.
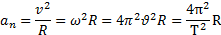

 .
.