НЕБЕСНАЯ МЕХАНИКА
Это повторение прошлогоднего успеха. Мы — маркетинг — благодарим всех, кто нам помогал и принял участие в выставке. Руководство компании. Менеджеров по продаже. Секретарей. Менеджеров по продуктам. Водителей. Нашу логистику. Финансистов. Всех, всех, всех... Всем — спасибо. Большое спасибо. Ваш Маркетинг. НЕБЕСНАЯ МЕХАНИКА ОГРАНИЧЕННАЯ ЗАДАЧА 3-х ТЕЛ
Кафедра астрономии Базей Александр Анатольевич Одесса 2001 ОГРАНИЧЕННАЯ ЗАДАЧА 3-х ТЕЛ. Точное аналитическое решение задачи 3-х тел не существует. Однако значительные успехи достигнуты при решении некоторых частных случаев задачи 3-х тел. Из частных случаев, имеющих непосредственные астрономические приложения, наиболее важен тот, когда одна из масс настолько мала, что не производит заметного влияния на движение двух других. Этот случай называется эллиптической ограниченной задачей 3-х тел или планетоидной задачей 3-х тел. Таким образом, в планетоидной задаче рассматривается движение тела, имеющего «бесконечно малую» массу, в поле тяготения 2-х тел с конечными массами, совершающих относительное движение по кеплеровым орбитам. Частный случай этой задачи, когда относительное движение происходит по круговым орбитам, называется ограниченной задачей 3-х тел. Постановка задачи Требуется найти движение тела P с бесконечно малой массой, притягиваемого двумя телами S и J, имеющими конечные массы и описывающими круговые орбиты вокруг общего центра инерции. {1} С математической точки зрения, бесконечно малое тело – это такое тело, которое притягивается конечными массами, но само их не притягивает. {2} С физической точки зрения, это тело настолько малой массы, что вызванные им возмущения в движении конечных тел, остаются меньше любой сколь угодно малой величины в течение сколь угодно большого промежутка времени. {3} Сила взаимного притяжения определяется из закона всемирного тяготения ускорение тела конечной массы Обозначим через m1 и m2 массы тел S и J. Не ограничивая общности, всегда можем считать, что Начнем рассмотрение в инерциальной системе координат. За начало координат примем общий центр масс О. Расстояние между телами конечных масс обозначим r12.
Координаты в абсолютной инерциальной системе отсчета:
Здесь
ВОПРОСЫ. 1. В чем заключается ограниченная задача 3-х тел? 2. Что называется бесконечно малым телом с математической точки зрения? 3. Что называется бесконечно малым телом с физической точки зрения? 4. Если масса одного из тел пренебрежимо мала, то сила притяжения его к другому телу из закона всемирного тяготения тоже пренебрежимо мала. Такое тело ни к чему не притягивается. В чем здесь ошибка?
Уравнения движения Из системы уравнений [1] (часть 1)
следует
Система дифференциальных уравнений [2] определяет движение тела Р (бесконечно малой массы). Движения тел S и J заданы по окружностям вокруг центра масс. Поскольку движения тел S и J описываются решением задачи 2-х тел, то они лежат в одной плоскости. Совместим их плоскость орбиты и плоскость xОh. Тогда в системе [2] z1 = z2 = 0:
Так как S и J движутся по окружностям, их движения равномерны, то можно перейти к вращающейся с угловой скоростью w системе координат XOY.
Проведем преобразование системы [3] к вращающейся системе координат.
Подставляя [5] в [3]:
Умножим 1-е уравнение на 1-е уравнение на
В этой системе координат оси OX и OY вращаются с постоянной угловой скоростью прямой, соединяющей тела S и J. Совместим с этой прямой ось OX, тогда y1 = y2 = 0:
где Это дифференциальные уравнения движения бесконечно малого тела Р, отнесенные к вращающимся осям так, что тела конечной массы всегда лежат на оси OX. Координаты тел S и J x1 и x2 явно от времени не зависят! {1} Правые части уравнений [7] можно представить в виде частных производных от силовой функции U: {2}
тогда
Это уравнения движения тела Р бесконечно малой массы во вращающейся с постоянной скоростью w системе координат. Общая задача определения движения тела Р – 6-го порядка, {3} то есть надо знать 6 интегралов движения в неинерциальной вращающейся системе координат.
ВОПРОСЫ. 1. Зависят ли во вращающейся системе отсчета координаты тел конечной массы от времени и почему? 2. Как определяется силовая функция в ограниченной задаче 3-х тел? 3. Сколько интегралов движения надо знать для определения движения тела бесконечно малой массы в ограниченной задаче 3-х тел? Интеграл Якоби Уравнения движения тела Р в форме [9] имеют интеграл, названный интегралом Якоби. Если уравнения системы [9] умножить соответственно на
Полученное уравнение может быть проинтегрировано, так как силовая функция U зависит только от координат x, y, z и явно от времени не зависит
Здесь V – скорость тела Р бесконечно малой массы во вращающейся системе отсчета. Выражение [10] называется интегралом Якоби. Он был открыт Якоби в 1836 году. Применение его к выяснению свойств движения тела Р было указано значительно позднее Хиллом. Смысл интеграла Якоби в том, что скорость тела бесконечно малой массы зависит только от координат и от расстояния до тел конечной массы. {2} Этот интеграл применяется строго в замкнутой системе 3-х тел, одно из которых, бесконечно малой массы. {3} Чтобы решить задачу полностью, надо найти еще 5 интегралов. Брунс доказал, что при употреблении прямоугольных координат не существует никаких новых алгебраических интегралов, а Пуанкаре показал, что при употреблении в качестве переменных элементов нет также новых однозначных трансцендентных интегралов.
ВОПРОСЫ. 1. При выводе интеграла Якоби из системы уравнений движения путем суммирования получают уравнение и интегрируют его. Почему это возможно? 2. В чем смысл интеграла Якоби? 3. Где применяется интеграл Якоби? Поверхности Хилла (поверхности нулевой скорости) Уравнение [10] дает соотношение между квадратом скорости и координатами тела Р относительно вращающихся осей. Поэтому, если постоянная интегрирования С определена численно начальными условиями, то уравнение [10] определяет скорость, с которой движется бесконечно малое тело во всех точках вращающегося пространства. Обратно, для данной скорости уравнение [10] дает геометрическое место точек относительного пространства, в которых может находиться бесконечно малое тело. {1} В частности, если скорость V в этом уравнении положить равной нулю, то оно определит поверхности, на которых скорость будет равна нулю. {2} С одной стороны от этих поверхностей скорость будет действительна, а с другой – мнима (так как V2 имеет разные знаки). {3}
Действительно, последнее слагаемое справа постоянное и отрицательное, а первые три слагаемых справа переменны и положительны. Если V2=0, то по разные стороны от этой поверхности V2 будет иметь противоположные знаки. Другими словами, тело Р может двигаться с одной стороны поверхности и не может двигаться с другой, где V2< 0. Несмотря на то, что вообще невозможно сказать какой будет орбита, все же это деление относительного пространства покажет, в каких частях бесконечно малое тело может двигаться и в каких частях не может в соответствии с выбранным значением постоянной С. Поверхность Хилла – это поверхность раздела областей возможного и невозможного движений тела бесконечно малой массы. {4} Никакой другой информации о траектории движения интеграл Якоби не дает. {5} Уравнение поверхностей нулевой относительной скорости имеет вид:
Изучим формы поверхностей нулевой скорости при различных значениях С. Так как в [12] входят только квадраты координат y и z, то поверхности нулевой скорости симметричны относительно плоскостей y=0 (xz) и z=0 (xy) {в [12] можно заменить y на -y, z на -z, не нарушая равенства}. Если массы тел S и J равны (m1 = m2), то поверхности симметричны и относительно плоскости x=0 (yz). Предположим сначала, что С очень большое число С=С1. В этом случае поверхность [12] состоит из трех отдельных поверхностей. В самом деле, левая часть уравнения может быть очень большой только в точках, в которых хотя бы один из трех членов этой части принимает очень большие значения. В точках, где
где e очень малая по сравнению с С1 положительная величина. Таким образом, поверхность [13] (назовем ее асимптотическим цилиндром) лежит внутри цилиндра Если r1 близко к нулю, то первое и третье слагаемое очень малы. Уравнение [12] принимает, следовательно, вид
где Уравнение [14] представляет замкнутую поверхность, заключающую точку S. При Третью часть поверхности нулевой скорости образует аналогичная квазисфера
окружающая точку J и вытянутая по направлению к точке S.
На рисунках 2.1, 2.2 и 2.3 представлены сечения координатными плоскостями поверхностей нулевой скорости в рассмотренном случае, когда постоянная Якоби С=С1 очень велика. Область невозможного движения расположена внутри асимптотического цилиндра, но вне квазисфер.
На рисунках 3.1, 3.2 и 3.3 показаны сечения поверхностей нулевой скорости для значения постоянной С=С2, при котором появляется общая точка у квазисфер. Дальнейшее уменьшение С приводит к слиянию квазисфер и образованию поверхности, имеющей форму гантели, с узкой перемычкой, через которую тело Р может перейти из окрестностей одного тела конечной массы в окрестности другого.
На рисунках 4.1, 4.2 и 4.3 показаны сечения поверхностей нулевой скорости для значения постоянной С=С3, при котором появляется общая точка у одной из квазисфер и асимптотического цилиндра.
На рисунках 5.1, 5.2 и 5.3 показаны сечения поверхностей нулевой скорости для малого значения постоянной С=С4, при котором рассматриваемые поверхности обратились в одну двуполостную. При дальнейшем уменьшении С полости этой поверхности уходят на бесконечность. Область невозможного движения сократилась до двух небольших несвязных областей. Те точки пространства OXYZ, в которых начинается слияние отдельных частей поверхностей нулевой скорости, являются, очевидно, особыми точками этих поверхностей. Поверхности [12] разделяют области возможного и невозможного движений. Вне асимптотического цилиндра [13] и внутри квазисфер [14] и [15] имеем V2> 0 {см. [11] - При уменьшении С область возможных движений будет расширяться {6} и при достаточно малых значениях С она будет заключать всю плоскость xy. Так при С=С4 движения будут невозможны на плоскости xy лишь внутри небольших областей, ограниченных кривыми, которые при дальнейшем уменьшении С будут сжиматься, обратятся в точки (указанные на рис.5.1 крестиками – это тоже особые точки), а затем совсем исчезнут. После этого поверхность нулевой скорости разделится на две не имеющие общих точек части, одна из которых будет находиться выше плоскости xy, а другая – ниже. Все вышеизложенное было впервые получено Хиллом и применено к движению Луны. Если, пренебрегая эксцентриситетом орбиты Земли, считать, что движение Луны (тело Р) удовлетворяет уравнениям ограниченной задачи 3-х тел, то ему соответствует значение постоянной Якоби, принадлежащее замкнутой кривой с максимальным расстоянием от центра Земли, равным 109.7 экваториального радиуса. Хилл сделал следующий вывод: «Таким образом, если пренебречь эксцентриситетом земной орбиты, мы имеем строгое доказательство существования верхнего предела радиус-вектора Луны». {7}
ВОПРОСЫ. 1. Верно ли утверждение, обратное интегралу Якоби? 2. Как определяется поверхность нулевой скорости? 3. Может ли тело Р пересечь поверхность нулевой скорости и почему? 4. Что такое поверхность Хилла? 5. Что говорит о траектории движения тела бесконечно малой массы интеграл Якоби? 6. С уменьшением константы Якоби область возможных движений тела бесконечно малой массы расширяется или сужается? 7. Каким образом Хилл обосновал существование верхнего предела радиус-вектора Луны? Особые точки поверхностей нулевой скорости Особые точки поверхности Для поверхностей нулевой скорости, уравнение которых имеет вид
особые точки даются уравнениями
Сравним правые части полученных уравнений с уравнениями движения тела бесконечно малой массы Р [7]:
Это уравнения, определяющие положения особых точек поверхностей нулевой скорости. По определению самих этих поверхностей
Итак, тело Р, имея соответствующее значение постоянной Якоби и оказавшись в особой точке, будет двигаться с нулевой скоростью и нулевым ускорением! {1} Особые точки поверхности нулевой скорости являются положениями относительного равновесия тела Р; в этих точках тело может находиться в равновесии относительно вращающейся системы координат. {2} Об устойчивости равновесия пока ничего сказано не было. Кроме того, выражения Особые точки поверхности нулевой скорости называют точками либрации или точками Лагранжа. {4} Где лежат особые точки? Третье уравнение системы [16] может быть удовлетворено только при z=0. Следовательно, все особые точки лежат в плоскости XOY – плоскости орбиты тел S и J. {5}
ВОПРОСЫ. 1. Как будет двигаться тело Р в особых точках поверхностей нулевой скорости? 2. Являются ли особые точки поверхностей нулевой скорости точками равновесия? 3. Если тело Р находится на поверхности нулевой скорости – как оно будет двигаться в последующие моменты времени? 4. Что такое точки либрации и точки Лагранжа? 5. Где лежат все особые точки? Коллинеарные точки Лагранжа Координаты особых точек являются решениями системы [16]:
Рассмотрим решения, когда
В знаменателях находятся положительные величины. Пусть e – малая положительная величина. Тогда при при при при при при Функция три раза меняет знак, переходя через ноль: Ø один раз между Ø Ø один раз между телом J и Поэтому на линии, соединяющей центры тел конечной массы S и J, имеется три особых точки. Это первая группа решений называется коллинеарными точками Лагранжа или коллинеарными точками либрации. {1}{2} Поскольку в уравнение [17], определяющее положение коллинеарных точек, входят массы тел, то их положение существенно зависит от соотношения масс в рассматриваемой системе тел. {3}
ВОПРОСЫ. 1. Где расположены коллинеарные точки Лагранжа? 2. Сколько известно коллинеарных точек Лагранжа? 3. Зависит ли положение коллинеарных точек Лагранжа от соотношения масс в системе 3-х тел? Компланарные (тригональные) точки Лагранжа Теперь найдем особые точки поверхностей нулевой скорости, не лежащие на оси OX:
Умножим 2-е уравнение на
Умножим 2-е уравнение на
Итак
Разделим 1-е уравнение системы [19] на 2-е уравнение системы [19] на
Из последней системы следует
Особые точки поверхностей нулевой скорости, не лежащие на оси OX равноудалены от тел S и J. Уточним их положение. Из первого уравнения следует
Вспомним [1]: Кроме того, выше было получено:
Перенесем
Особые точки образуют равносторонние треугольники с телами S и J независимо от их относительных масс. Это вторая группа решений называется компланарными точками Лагранжа или компланарными точками либрации. Их две. {1} {2} {3} Таким образом, определено положение всех 5-ти особых точек. {4}
ВОПРОСЫ. 1. Где расположены компланарные точки Лагранжа? 2. Сколько известно компланарных точек Лагранжа? 3. Зависит ли положение компланарных точек Лагранжа от соотношения масс в системе 3-х тел? 4. Сколько всего точек Лагранжа?
Дополнительное рассмотрение: линии Хилла в плоскости орбиты Вернемся к системе [12], определяющей поверхности Хилла:
Линии нулевой скорости в плоскости орбиты XOY наиболее интересны, поскольку именно здесь расположены все особенности. Уравнение линий в плоскости XOY:
Если это уравнение рационализировать и освободить от дробей, то получим многочлен 16-й степени относительно х и у. Если значение одной их переменных взято произвольно, то соответствующее значение другой может быть найдено путем решения этого уравнения численными методами. Можно избегнуть трудностей численного решения преобразованием уравнения в биполярные координаты, то есть точки кривых могут быть определены расстояниями от двух фиксированных точек {1} – полюсов на оси ОХ. Этот метод неприменим, если кривые не симметричны относительно оси, на которой лежат полюса.
Вспомним
Заметим следующее -
последнее слагаемое равно 0 по выбору начала системы отсчета,
Уравнение [22] можно переписать
Если взято произвольное значение r2, то из этого уравнения может быть вычислено r1; точками пересечения окружностей с центрами в S и J с соответственно вычисленными значениями радиусов r1 и r2 будут точки на линиях нулевой скорости. Перепишем уравнение [24] в виде (r2 фиксировано!)
Так как Из уравнения [24] следует, что
Предположим, что это неравенство удовлетворено. Тогда корни уравнения [25] можно получить следующим образом:
Совершенно аналогичное уравнение справедливо, если r1 фиксировано и вычисляется r2:
Проведем следующее преобразование
В предельном случае неравенство, определяющее три действительных корня, переходит в равенство
Подставим это в первое слагаемое в коэффициенте
Поэтому, в пределе (
Решение этого уравнения определяет то крайнее значение r2, для которого [25] имеет действительные корни. Условие, при котором уравнение [27] будет иметь действительные корни, аналогично [26] запишется в виде:
подставляя вместо
Поэтому, чтобы линии нулевой скорости имели действительные точки в плоскости XOY, С’ должно быть больше, в крайнем случае, равно значению, определяемому формулой [28]. Возвращаясь к [23], имеем
Для полученного значения константы Якоби C уравнение [23] примет следующий вид:
легко проверить, что данное уравнение выполняется при Константа Якоби C’, определяемая равенством [28] соответствует поверхности Хилла, проходящей через компланарные точки Лагранжа L4 и L5.
ВОПРОСЫ. 1. Дайте понятие биполярных координат.
Критерий Тиссерана Интеграл Якоби был использован при решении вопроса о тождественности вновь открытой периодической кометы с кометой ранее наблюдавшейся. Такой вопрос далеко не всегда может быть решен путем простого сравнения элементов орбит, так как в случае прохождения кометы вблизи одной из больших планет ее орбита может измениться до неузнаваемости. {1} Конечно, вопрос всегда может быть решен путем вычисления возмущений одной из комет за истекший промежуток времени. Но это весьма трудоемкая операция. Большие изменения элементов происходили всегда при прохождении кометы очень близко от Юпитера. Именно за короткое время (не превышающее нескольких месяцев) пребывания кометы вблизи Юпитера и происходят те большие изменения элементов орбиты, по сравнению с которыми возмущения, производимые остальными планетами, уже не имеют существенного значения. С другой стороны, прохождения кометы вблизи других планет столь маловероятны, что до середины ХХ века не наблюдались ни разу. {2} Все это показывает, что движение комет с интересующей нас точки зрения можно уподобить, если пренебречь эксцентриситетом орбиты Юпитера, движению бесконечно малой массы в ограниченной задаче 3-х тел. Таким образом, координаты кометы (x, y, z) должны удовлетворять, каковы бы ни были ее возмущения со стороны Юпитера, интегралу Якоби
или
здесь
При вычислении постоянной Якоби С по формуле [29] надо брать координаты и составляющие скорости Если время t считать от того момента, когда ось Ox совпадает с Sx, то формулы перехода запишутся так:
где x1 – координата т. S (x1< 0) – расстояние SO – от центра Солнца до центра масс системы. Дифференцируя
Тогда левая часть уравнения [29]:
Первое слагаемое справа в уравнении [29]:
В неподвижной системе отсчета уравнение [29] принимает вид
или
Если a, p, e, i – оскулирующие элементы орбиты кометы в её движении относительно Солнца, то из интеграла площадей [37](часть 2) из интеграла энергии [33](часть 2) где
Разделим это уравнение на
Вспомним [1]:
|

 . В нашем рассмотрении одна из масс m Þ 0. Поэтому ускорение тела бесконечно малой массы
. В нашем рассмотрении одна из масс m Þ 0. Поэтому ускорение тела бесконечно малой массы  ,
,  ;
; ,
,  . {4}
. {4} .
. Тела конечной массы S и J вращаются вокруг центра масс по окружностям с постоянной угловой скоростью w. Из третьего закона Кеплера [36.1] (часть 2)
Тела конечной массы S и J вращаются вокруг центра масс по окружностям с постоянной угловой скоростью w. Из третьего закона Кеплера [36.1] (часть 2)  ,
,  ,
, [1]
[1]
 расстояние тел S и J от тела бесконечно малой массы Р,
расстояние тел S и J от тела бесконечно малой массы Р, расстояние тела Р от начала системы отсчета.
расстояние тела Р от начала системы отсчета.

 [2]
[2]

 [4]
[4] [5]
[5]
 , 2-е -на
, 2-е -на 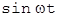 и сложим;
и сложим; , 2-е -на
, 2-е -на  [6]
[6] [7]
[7]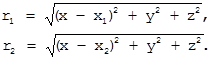
 [8]
[8] [9]
[9] и сложить, то
и сложить, то
 . {1} Выражение в скобках справа представляет собой полную производную. Получим
. {1} Выражение в скобках справа представляет собой полную производную. Получим
 , где С – постоянная интегрирования.
, где С – постоянная интегрирования. [10]
[10]
 [11]
[11] [12]
[12] очень велико, второе и третье слагаемые очень малы, так что уравнение можно записать так:
очень велико, второе и третье слагаемые очень малы, так что уравнение можно записать так: , [13]
, [13] и асимптотически к нему приближается.
и асимптотически к нему приближается. , [14]
, [14] и очень мало по сравнению с С1.
и очень мало по сравнению с С1. эта поверхность в пределе обращается в сферу бесконечно малого радиуса с центром в S (назовем ее квазисферой). Легко видеть, что квазисфера [14] целиком заключает внутри себя сферу
эта поверхность в пределе обращается в сферу бесконечно малого радиуса с центром в S (назовем ее квазисферой). Легко видеть, что квазисфера [14] целиком заключает внутри себя сферу  , причем больше всего она удаляется от этой сферы в плоскости xy {z=0, поэтому вклад первого слагаемого в
, причем больше всего она удаляется от этой сферы в плоскости xy {z=0, поэтому вклад первого слагаемого в  максимальный}, а особенно – по направлению к точке J {r1 минимально, поэтому вклад третьего слагаемого в
максимальный}, а особенно – по направлению к точке J {r1 минимально, поэтому вклад третьего слагаемого в  , [15]
, [15]












 определяются, как известно, уравнениями
определяются, как известно, уравнениями  .
. [12]
[12] [16]
[16]
 . Поэтому
. Поэтому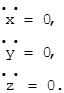
 пропорциональны направляющим косинусам нормали во всех обыкновенных точках поверхности
пропорциональны направляющим косинусам нормали во всех обыкновенных точках поверхности  . {Вспомним – уравнение нормали к поверхности
. {Вспомним – уравнение нормали к поверхности  , где a, b, c – текущие координаты нормали} Поэтому если бесконечно малое тело Р оказалось на поверхности нулевой скорости, то оно начнет двигаться в направлении нормали. {3} В особых точках положение нормали становится двойным и там тело Р может оставаться в покое относительно вращающейся системы координат.
, где a, b, c – текущие координаты нормали} Поэтому если бесконечно малое тело Р оказалось на поверхности нулевой скорости, то оно начнет двигаться в направлении нормали. {3} В особых точках положение нормали становится двойным и там тело Р может оставаться в покое относительно вращающейся системы координат. [16]
[16] . В этом случае искомые особые точки лежат на оси OX и их абсциссы удовлетворяют уравнению
. В этом случае искомые особые точки лежат на оси OX и их абсциссы удовлетворяют уравнению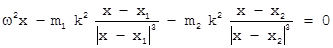 [17]
[17]
 и левая часть уравнения
и левая часть уравнения  ;
; ,
, 
 ,
, 
 ,
,  ,
,  ,
,  и телом S;
и телом S; один раз между телом S и телом J;
один раз между телом S и телом J; .
. . В этом случае 2-е уравнение системы [16] можно разделить на y:
. В этом случае 2-е уравнение системы [16] можно разделить на y: [18]
[18]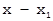 и вычтем из 1-го:
и вычтем из 1-го:

 .
. и вычтем из 1-го:
и вычтем из 1-го:

 .
. [19]
[19] Отметим, что
Отметим, что  , а
, а  . Кроме того, поскольку начало системы отсчета совпадает с центром масс системы тел S и J, то
. Кроме того, поскольку начало системы отсчета совпадает с центром масс системы тел S и J, то  ;
;  .
. ;
; . Получим
. Получим Далее
Далее 
 . [20]
. [20] .
. . [1]
. [1] .
. влево:
влево:  ,
, . Но
. Но  , подставляя
, подставляя , итак
, итак , а следовательно
, а следовательно  [21]
[21]
 .
. Пусть центры тел S и J совпадают с полюсами; расстояния от этих точек соответственно равны r1 и r2. Для перехода в биполярные координаты надо выразить x2+y2 через эти величины.
Пусть центры тел S и J совпадают с полюсами; расстояния от этих точек соответственно равны r1 и r2. Для перехода в биполярные координаты надо выразить x2+y2 через эти величины. [1]. Тогда
[1]. Тогда . [22]
. [22]

 ,
, .
. ,
, [23]
[23] . [24]
. [24] ,
, ,
, , где
, где  . [25]
. [25] , то имеется хотя бы один действительный отрицательный корень уравнения [25] при любом значении а. Но r1 существенно положительная величина, поэтому нас интересуют только положительные решения.
, то имеется хотя бы один действительный отрицательный корень уравнения [25] при любом значении а. Но r1 существенно положительная величина, поэтому нас интересуют только положительные решения. при любых r1 и r2, а значит коэффициент а< 0. В теории алгебраических уравнений доказывается, что кубичное уравнение такой формы имеет три различных действительных корня, если
при любых r1 и r2, а значит коэффициент а< 0. В теории алгебраических уравнений доказывается, что кубичное уравнение такой формы имеет три различных действительных корня, если  , или
, или


 , поскольку всегда а< 0, то второй сомножитель положителен. Поэтому неравенство будет выполнено при
, поскольку всегда а< 0, то второй сомножитель положителен. Поэтому неравенство будет выполнено при . [26]
. [26]
 ,
, ,
, , где r11, r12, r13 – три корня кубичного уравнения [25].
, где r11, r12, r13 – три корня кубичного уравнения [25]. , где
, где 
 .
. , что позволяет (в пределе!):
, что позволяет (в пределе!): разделим на
разделим на 
 .
. , получим
, получим .
. . [27]
. [27] ;
; его значение и сохраняя только знак равенства, получим
его значение и сохраняя только знак равенства, получим разделим на
разделим на  ,
, ,
, . [28]
. [28] ,
,  .
. ,
,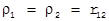 , то есть поверхности исчезают с плоскости XOY в точках, образующих равносторонние треугольники с массами m1 и m2.
, то есть поверхности исчезают с плоскости XOY в точках, образующих равносторонние треугольники с массами m1 и m2. , [29]
, [29] есть среднее суточное движение Юпитера,
есть среднее суточное движение Юпитера,  и
и  - расстояния кометы от Солнца и Юпитера.
- расстояния кометы от Солнца и Юпитера. Отсюда необходимое условие тождественности двух комет – две наблюдавшиеся в разное время кометы могут оказаться тождественными только в том случае, когда вычисленные для них постоянные Якоби достаточно мало отличаются между собой. {3}
Отсюда необходимое условие тождественности двух комет – две наблюдавшиеся в разное время кометы могут оказаться тождественными только в том случае, когда вычисленные для них постоянные Якоби достаточно мало отличаются между собой. {3} относительно вращающейся системы отсчета с центром в т.О. Для упрощения этих вычислений, перейдем к гелиоцентрической системе отсчета (с центром в т.S) Sxhz с неизменным направлением осей, в которой ось Sz параллельна оси Oz.
относительно вращающейся системы отсчета с центром в т.О. Для упрощения этих вычислений, перейдем к гелиоцентрической системе отсчета (с центром в т.S) Sxhz с неизменным направлением осей, в которой ось Sz параллельна оси Oz.
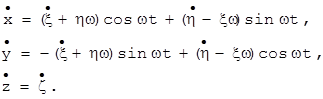





 ;
;


 ;
;


 ,
, ,
, ,
,  , поскольку рассматриваем движение кометы относительно Солнца. Тогда последнее равенство перепишется
, поскольку рассматриваем движение кометы относительно Солнца. Тогда последнее равенство перепишется


 и перенесем константу влево:
и перенесем константу влево: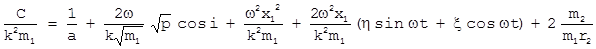
 , где
, где .
.


