Основные свойства функций. Функцию , определенную на симметричном относительно нуля множестве Х, называют четной, если для любого верно равенство
Четность Функцию Если функция не является ни четной, ни нечетной, то ее называют функцией общего вида, или говорят, что функция свойством четности не обладает. График четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат.
Периодичность Число Функцию, имеющую период называют периодической. Если Т – период функции, то для любого Если функция имеет наименьший положительный период, то он берется в качестве основного. График периодической функции с периодом Т функции при сдвиге вдоль оси абсцисс на Т переходит в себя. Тригонометрические функции
Пример 1. Исследовать функции на четность: а) в) Решение. а) Функция определена при Значит,
б) Функция определена при
в) Хотя формально
Пример 2. Определить, какие из функций являются периодическими, указать их наименьший период: а) г) Решение. а) периодическая,
б) периодическая,
в) непериодическая;
г) периодическая,
д) непериодическая;
е) периодическая,
Самостоятельная работа.
Вариант 1. 1. Исследовать функции на четность: а) в) 2. Найти основной период функции:
Вариант 2. 1. Исследовать функции на четность: а) б) 2. Найти основной период функции:
Вариант 3. 1. Исследовать функции на четность: а) 2. Найти основной период функции:
Ответы. Вариант 1: 1а)четная; б)нечетная; в) общего вида; 2) Вариант 2: 1а)нечетная; б) четная; в) общего вида; 2) Вариант 3: 1а) четная; б)нечетная; в) общего вида; 2)
Дополнительные упражнения. 1. Найти область определения функции: а) б) д) 2. Исследовать функции на четность: а) б) 3. Найти основные периоды функций: а) в)
Ответы.
1.а) г) 2.а) четная; б) общего вида; в) четная; г) четная. 3. а)
|

 , определенную на симметричном относительно нуля множестве Х, называют четной, если для любого
, определенную на симметричном относительно нуля множестве Х, называют четной, если для любого  верно равенство
верно равенство  , и называют нечетной, если для любого
, и называют нечетной, если для любого 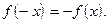
 называют периодом функции f(x), если для любого
называют периодом функции f(x), если для любого  выполнены условия
выполнены условия  и
и  .
. число nT также является периодом этой функции.
число nT также является периодом этой функции. и
и  - периодические с основным периодом T =
- периодические с основным периодом T = 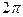 , а
, а  и
и  - с основным периодом T = p.
- с основным периодом T = p. ; б)
; б)  ;
; при
при 
 , т.е. на множестве, симметричном относительно начала координат и
, т.е. на множестве, симметричном относительно начала координат и  .
. , т.е. на промежутке, симметричном относительно 0;
, т.е. на промежутке, симметричном относительно 0; Значит,
Значит,  , но эта функция не обладает свойством четности, т.к. ее область определения
, но эта функция не обладает свойством четности, т.к. ее область определения  несимметрична относительно начала координат.
несимметрична относительно начала координат. , б)
, б)  , в)
, в)  ,
, , д)
, д)  , е)
, е)  .
. , т.к. у функции
, т.к. у функции  , откуда
, откуда  ;
; , т.к. у функции
, т.к. у функции  , то
, то  , откуда
, откуда  ;
; ;
; .
. ; б)
; б)  ;
; .
. .
. ;
; ; в)
; в)  .
.
 ; б)
; б) 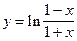 ; в)
; в)  .
. .
. ;
; ;
;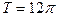 .
. ;
; ; в)
; в)  ; г)
; г)  ;
; .
. ;
; ; в)
; в)  ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ; в)
; в)  ;
;
 ; д)
; д)  .
. ; в)
; в)  ; г)
; г) 


