Лабораторная работа № 5. Составление программ обработки двумерных массивов
Цель работы: овладеть навыками алгоритмизации и программирования структур с вложенными циклами, особенностями обработки двумерных массивов, способами их ввода и вывода.
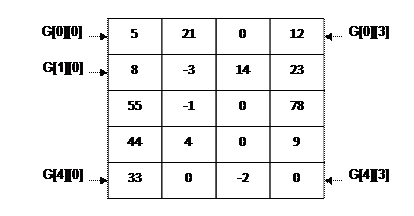
Краткие теоретические сведения Массивы в программах C++ могут быть не только линейными. Довольно частым является использование двух - (и более) -мерных структур. К примеру, прямоугольная матрица – типичная структура, представимая с помощью двумерного массива. Многомерный массив в C++ организован по принципу «массива массивов» (рис. 6). Общий формат его объявления: тип имя[N1][N2]…[NM];
Рис. 6. Пример двумерного массива Здесь M – число индексов (или размерность) массива. Индексы изменяются в пределах от 0 до N1 – 1, от 0 до N2 – 1, от 0 до N3 – 1,..., от 0 до NM – 1, соответственно. К примеру, запись int G[5][4]; означает объявление двумерного массива целых чисел с именем G и размерами 5´ 4. Доступ к элементам многомерного массива в программе производится так же, как и в одномерном случае, то есть путем указания имени массива и набора индексов в квадратных скобках. Например, операция присваивания значения 0 последнему элементу будет записана как G[4][3] = 0. При работе с многомерными массивами удобно использовать вложенные циклы for. С их помощью можно выполнить заданное действие с каждым из элементов массива путем перебора всех значений индексов. Приведенный ниже фрагмент программного кода выводит на экран все элементы массива G. for(int i=0; i< 5; i++) // цикл по строкам i { for(int j=0; j< 4; j++) // цикл по строкам j cout < < G[i][j] < < “\t”; // выводим G[i][j] cout < < endl; // перевод на новую строку }
Рис. 7. Блок – схема вывода элементов массива на экран Здесь внешний цикл по I последовательно пробегает все значения от 0 до 5. При каждом i запускается внутренний цикл по j от 0 до 4. В теле этого цикла на экран выводятся значение элемента G[i][j] и знак табуляции (горизонтальный отступ). Внутренний цикл продолжается до тех пор, пока не будут перебраны все значения j, то есть не будет выведена вся i -я строка. По завершении внутреннего цикла, экранный курсор перемещается на новую строку манипулятором endl, и далее внешний цикл продолжает свою работу, последовательно выводя на экран другие строки массива.
Задание 1. Изучить: правила организации вложенного цикла с учетом порядка перебо- ра элементов матрицы; правила использования приемов программирования в структурах с вложенными циклами; способы ввода и вывода матриц, имеющиеся в языке программирования. 2. Разработать алгоритм решения в соответствии с заданием. 3. Составить программу решения задачи.
Пример выполнения работы
Условие: Имеется вещественная квадратная матрица размером 4´ 4. Напишите программу, вычисляющую произведение элементов в каждой ее строке. Матрица вводится с клавиатуры. #include < conio.h> #include < iostream.h> void main(void) { float X[4][4]; // объявляем массив 4´ 4 for(int i=0; i< 4; i++) for(int j=0; j< 4; j++) { cout < < " input X[" < < i < < ", " < < j < < " ] = "; cin > > X[i][j]; // вводим элементы матрицы } cout < < " \n Results: \n"; for(int i=0; i< 4; i++) // цикл по строкам { float P = 1.0; // вспомогательная переменная for(int j=0; j< 4; j++) // цикл по элементам в строке P = P * X[i][j]; // домножаем P на X[i][j] cout < < " \n proizvedenie " < < i < < " -i stroki = " < < P; // выводим результат на экран } getch(); } Условие: Дана квадратная матрица размером N x N. Переставить элементы верхнего треугольника матрицы с соответствующими элементами нижнего треугольника. Начальные данные: 1. константа n, которая определяет размер матрицы; 2. двумерный массив размерности n; 3. параметр i для цикла по строкам; 4. параметр j для цикла по столбцам; 5. параметр r для промежуточной информации. Результат вычисления: новая матрица с переставленными элементами. #include< stdio.h> #include< conio.h> #include< iostream.h> void main(void) { const n = 2; int i, j, a[n][n]; int r; clrscr(); printf (" Введи элементы матрицы: \n"); for (i = 0; i < = n-1; i++) for (j = 0; j < = n-1; j++) { printf(" a(%d, %d)= ", i, j); scanf(" %d", & a[i][j]); } cout < < " Введена матрица: \n"; for (i = 0; i < n; i++) { for (i = 0; j < n; j++) printf(" %d ", a[i][j]); printf(" \n"); } for (i = 0; i < = n/2; i++) for (j = i; j < = n-1-i; j++) { r = a[i][j]; a[i][j] = a[n-1-i][j]; a[n-1-i] [j]=r; } cout < < " \n\nМатрица после перестановки: \n"; for (i = 0; i < = n-1; i++) { for (j = 0; j < = n-1; j++) printf(" %d ", a[i][j]); printf(" \n"); } getch(); } Условие: Пусть Искомое произведение
#include < conio.h> #include < iostream.h> const int N = 3; // используем константу N=3 void main(void) { float A[N][N] = { {1, 1, 1}, {2, 2, 2}, {3, 3, 3} }; // исходная матрица A float B[N][N] = { {1, 2, 3}, {1, 2, 3}, {1, 2, 3} }; // исходная матрица B float C[N][N]; // матрица произведения С for(int i=0; i< N; i++) // цикл по строкам С { for(int j=0; j< N; j++) // цикл по столбцам С { float s = 0.0; // вспомогательная переменная for(int k=0; k< N; k++) // цикл суммирования по k s += A[i][k]*B[k][j]; // добавляем к s новое слаг-ое C[i][j] = s; // записываем s в C[i][j] } } cout < < " Results: \n"; // далее выводим C на экран for(int i=0; i< N; i++) { for(int j=0; j< N; j++) cout < < C[i][j] < < " \t"; cout < < endl; } getch(); }
Задания для самостоятельного выполнения 1. Для заданного двумерного числового массива подсчитать количество строк, состоящих только из ненулевых элементов. 2. Для заданного двумерного числового массива подсчитать количество столбцов, состоящих только из отрицательных элементов. 3. Для заданного двумерного числового массива подсчитать количество таких строк, в которых положительных элементов больше, чем отрицательных. 4. Для заданного двумерного числового массива подсчитать количество таких столбцов, у которых максимальный элемент этого столбца расположен в первой строке. 5. Для заданного двумерного числового массива подсчитать количество таких столбцов, у которых максимальный элемент этого столбца единственный. 6. Для заданного двумерного числового массива подсчитать количество таких столбцов, у которых максимальный элемент этого столбца расположен в первой строке. 7. Дана целочисленная матрица размера M x N. Найти количество ее строк столбцов, все элементы которых различны. 8. Дана квадратная матрица. Найти максимальное значение из элементов, расположенных в левом нижнем углу. 9. Дана квадратная матрица порядка M. Найти суммы элементов ее диагоналей, параллельных главной побочной (начиная с одноэлементной диагонали A[1, M]1|A[1, 1]2). 10. Дана квадратная матрица порядка M. Заменить нулями элементы, лежащие одновременно выше ниже главной диагонали (включая эту диагональ) и выше ниже побочной диагонали (также включая эту диагональ). 11. Дана квадратная матрица порядка M. Зеркально отразить ее элементы относительно [горизонтальной оси симметрии] [вертикальной оси симметрии] [главной диагонали] [побочной диагонали] матрицы. 12. Дана квадратная матрица порядка M. Повернуть ее на 90о, 180о, 270о в положительном направлении. 13. Дана матрица размера N x M. Вывести количество строк столбцов, элементы которых монотонно возрастают, убывают. 14. Дана матрица размера N x M. Найти минимальный, максимальный среди элементов тех строк столбцов, которые упорядочены либо по возрастанию, либо по убыванию. 15. Дана матрица размера N x m. Поменять местами строки столбцы, содержащие минимальный и максимальный элементы матрицы. 16. В матрице А (m, n) найти строку с максимальной суммой элементов и строку с минимальной суммой элементов. Далее сформировать вектор В (2, m), у которого бы элементы чередовались с максимальной и минимальной строками. 17. Дана действительная квадратная матрица. Требуется преобразовать матрицу: поэлементно вычесть последнюю строку из всех строк, кроме последней. Контрольные вопросы 1. Указать основные правила организации вложенных циклов. 2. Указать способы выхода из внутреннего цикла. 3. Как организовать вывод матрицы в общепринятом виде? 4. Как организовать вывод нижней треугольной матрицы в общепринятом виде? 5. Как организовать ввод матрицы размером N x M элементов? 6. Верно ли утверждение, что индекс массива должен иметь тип float.
|


 Алгоритм работы этого фрагмента иллюстрируется следующей блок-схемой (рис. 7).
Алгоритм работы этого фрагмента иллюстрируется следующей блок-схемой (рис. 7).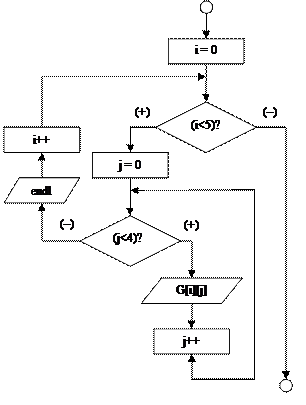
 и
и 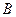 – две квадратные матрицы размером 3´ 3. Требуется написать программу, рассчитывающую их произведение
– две квадратные матрицы размером 3´ 3. Требуется написать программу, рассчитывающую их произведение 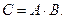
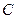 – это также матрица 3´ 3, элементы которой рассчитываются по формуле
– это также матрица 3´ 3, элементы которой рассчитываются по формуле 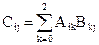 (
(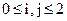 ).
).


