Магнитные поля асинхронных двигателей. Вращающееся магнитное поле
Принцип действия асинхронных двигателей базируется на взаимодействии вращающегося магнитного поля и короткозамкнутых обмоток или элементов, приравненных к ним. Поэтому проблема получения вращающегося поля в магнитной системе машины является основной. В большинстве случаев для получения вращающегося магнитного поля используется трехфазная система источников питания, которая и получила широкое распространение. Но не следует забывать о том, что существуют и другие способы получения магнитных полей, близких к вращающимся магнитным полям. Что же такое идеальное вращающееся магнитное поле?
Вращающимся магнитным полем называют такое магнитное поле, которое, не изменяя своей конфигурации и интенсивности, вращается в пространстве вокруг оси, перпендикулярной силовым линиям и являющейся осью симметрии поля. Наглядным примером такого поля является поле постоянного магнита (рис. 6.1), вращающегося вокруг собственной оси симметрии OO ’. Магнитная индукция поля в любой точке постоянного магнита, как и величина магнитного потока магнитопровода остаются неизменными, но направление этих величин изменяется в соответствии с законом вращения этого магнита. Способы получения вращающегося магнитного поля различны. Наиболее простым из них является использование трехфазной системы напряжений, с помощью которой можно достаточно легко получить намагничивающие силы равной величины с фазовым сдвигом, равным трети периода. Расположим три прямоугольные рамки в пространстве так, чтобы угол между плоскостями, составил 120 ° (рис. 6.2).
Рис. 6.2
Стороны рамок, параллельные оси OO’, обозначим буквами AX, BY и CZ. Рассмотрим суммарное магнитное поле трех рамок, по которым протекают токи, изменяющиеся во времени по синусоидальному закону, но сдвинутые во времени на треть периода. Индексы токов выберем в соответствии с обозначением, принятым Эти токи, как было уже сказано, изменяются во времени по законам синуса, т. е.
Условимся под положительным направлением токов понимать такое направление токов рамок, когда в сторонах A, B, C ток идет от читателя, а в сторонах X, Y, Z - к читателю. Временная диаграмма токов представлена на рис. 6.3.
Рис. 6.3
В дальнейших рассуждениях будем считать, что магнитный поток рамки пропорционален току этой рамки, а его направление определяется известным правилом буравчика. Магнитные потоки рамок будем представлять векторами, перпендикулярными плоскостям рамок. Длины векторов пропорциональны мгновенным значениям магнитных потоков рамок. Мгновенные значения потоков рамок могут быть найдены из формул
Определим магнитный поток системы рамок, питаемых трехфазной системой токов. В момент времени t = 0 ток фазы A равен нулю, ток фазы B имеет отрицательное направление, ток фазы C положителен. Магнитный поток рамки A равен нулю, магнитный поток рамки B Магнитный поток фазы C Результирующий магнитный поток
его направление показано на рис. 6.4, a.
а б в Рис. 6.4
Рассмотрим магнитный поток рамок в момент времени t = t 1(рис. 6.4, б). В этот момент времени ток рамки A положительный, ток рам-ки B отрицательный и ток фазы C положительный. Фаза токов увеличилась на 30 °. Магнитные потоки рамок
Магнитные потоки рамок представлены векторами на рис. 6.4, б. Суммарный магнитный поток В момент времени t = t 2, соответствующий изменению фазы токов на 60 ° (рис. 6.4, в), ток рамки A положительный, ток фазы C равен нулю и ток фазы B отрицательный, что отражено на рис. 6.4, в знаками (+) и (·) на сечении проводников рамок. Длина векторов магнитных потоков определяется с помощью формул
Длина суммарного магнитного потока Как и в предыдущие моменты времени, суммарный магнитный поток сохранил свою величину. Направление вектора этого потока изменилось на 60 °. Очевидным является то, что за время, равное периоду, магнитное поле рамок, сохраняя свою конфигурацию и интенсивность, повернется в пространстве на 360 градусов или сделает полный оборот. Если частота питающих токов будет равна 50 герцам, то за одну секунду поле сделает 50 оборотов, а за минуту - 3000 оборотов. Магнитное поле трех рамок, питаемых трехфазной системой токов, представленное магнитными силовыми линиями, изображено на рис. 6.5, a. Такое поле называют двухполюсным. Расположим шесть рамок в пространстве так, как это изображено на рис. 6.5, б. В данном случае обмотка каждой фазы состоит из двух рамок. При этом рамки одной фазы расположены соосно
а б Рис. 6.5
Направление токов в рамках в момент времени t 1 в соответствии с временной диаграммой токов (см. рис. 6.4) представлено соответствующими символами (+) и (·) на рис. 6.5, б. Результирующее магнитное поле представлено силовыми линиями. Такое магнитное поле называется четырехполюсным. Не составляет труда показать, что за один период колебаний токов магнитное поле Таким образом, изменяя конфигурацию обмоток, образующих магнитное поле, можно изменять ее частоту вращения. В общем случае частота вращения магнитного поля прямо пропорциональна частоте питающих токов и обратно пропорциональна числу пар полюсов этого поля, т. е. Для изменения частоты вращения магнитного поля можно изменить частоту питающего напряжения. Это наиболее очевидное решение вопроса изменения частоты вращения магнитного поля, которое связано с необходимостью создания специального источника трехфазного напряжения регулируемой частоты. Другим способом изменения частоты вращения поля является укладка в пазы статора такой обмотки, которая создала бы число пар полюсов больше одной. Тогда за один период изменения питающего напряжения поле повернется не на 360 ° в пространстве, а на 180, 120, 90 ° в зависимости от количества периодов укладки обмотки по Магнитное поле асинхронных двигателей, работающих в реальных условиях, не всегда является круговым вращающимся, т. е. таким, когда величина магнитного потока одного полюса результирующего поля не зависит от времени. В ряде случаев используется пульсирующее магнитное поле. Такое магнитное поле может быть образовано однофазной обмоткой, расположенной на статоре и питаемой источником однофазного синусоидального тока. На рис. 6.6 и 6.7, a представлен пример расположения однофазной обмотки на статоре, образующей поле с одной парой полюсов, и на рис. 6.7, б - схема расположения проводников однофазной обмотки, образующей две пары полюсов. И в том, и в другом случае магнитное поле будет пульсирующим.
а б Рис. 6.6 Рис. 6.7
Круговое вращающееся магнитное поле может быть получено с помощью двухфазной системы токов, т. е. токов, сдвинутых по фазе на четверть периода. Рассмотрим магнитное поле двух рамок с токами, изменяющимися во времени по косинусному закону и расположенными Ток рамки AX - Ток рамки BY - Пусть ток рамки AX сдвинут по фазе относительно тока рам-
Представим потоки рамок в векторной форме, совместив плоскость поперечного сечения рамок с комплексной плоскостью так, что действительная ось будет расположена в плоскости рамки AX, а мнимая - в плоскости рамки BY, как показано на рис. 6.6. Вектор суммарного магнитного потока определится в этом случае из уравнения
или
Модуль вектора магнитного потока
Аргумент вектора W t, определяющий его направление на комплексной плоскости, совпадает с его направлением в пространстве
Очевидно то, что величина магнитного потока остается постоянной, а его направление определяется углом W е = w t. Частота вращения полученного магнитного поля в пространстве равна угловой частоте питающих токов. Другими словами, магнитное поле двух рамок, расположенных в пространстве под 90 ° и питаемых токами с фазовым сдвигом в четверть периода, является круговым вращающимся полем. 6.2. Эллиптические и пульсирующие магнитные Представление магнитных потоков рамок в векторной форме и совмещение плоскости сечения системы рамок с комплексной плоскостью очень удобно для анализа магнитного поля электрических машин. Рассмотрим магнитное поле тех же рамок (см. рис. 6.6), питаемых токами одной частоты, но имеющих разные амплитуды с произвольным фазовым сдвигом a. Пусть токи рамок изменяются по косинусным законам во времени Будем считать, что мгновенные значения потоков пропор-циональны мгновенным значениям токов, т. е. Вектор потока Ф B совпадает по направлению с действительной осью, а
Из курса математики известна взаимозависимость тригонометрических и гиперболических функций, в соответствии с которыми
Таким образом, вектор результирующего магнитного потока двух рамок, питаемых токами различной амплитуды и сдвину- Рассмотрим магнитный поток для нескольких вариантов соотношений амплитуд токов рамок и значений фазового сдвига. 1. Пусть Следовательно, мы будем иметь круговое вращающееся магнитное поле с частотой вращения в пространстве W. 2. Пусть в этом случае
Таким образом, при питании рамок токами равных амплитуд На комплексной плоскости потоки рамок и результирующий магнитный поток представлены векторами прямого поля Как уже ранее утверждалось, пульсирующее поле может быть представлено в виде суммы двух круговых вращающихся магнитных полей равных амплитуд и противоположного направления вращения. Достаточно легко показать то, что при a = 0 при любом соотношении амплитуд токов суммарное магнитное поле будет пульсирующим, а максимальная величина потока определяется из уравнения 3. Рассмотрим случай равенства амплитуд токов обмоток при изменяющемся фазовом сдвиге фаз токов a (рис. 6.8).
Рис. 6.8
При
=
Результирующий магнитный поток При изменении a от нуля до Магнитный поток обратного поля Таким образом, увеличение фазового сдвига токов от a = 0 В общем случае при произвольном значении a амплитуда потока прямого поля не равняется амплитуде обратного поля. Конец вектора магнитного потока результирующего магнитного поля опишет эллипс на комплексной плоскости (рис. 6.9). Магнитное поле, магнитный поток которого может быть представлен вращающимся вектором с изменяющейся длиной, а годограф которого представляет собой эллипс, называют эллиптическим. Такое поле, как и в предыдущем случае, может быть представлено в виде суммы двух круговых вращающихся магнитных полей с разными величинами магнитных потоков.
Такое изменение магнитного поля при изменении фазового сдвига токов используется для фазового регулирования частоты вращения управляемого асинхронного двигателя. 4. Рассмотрим магнитное поле при фазовом сдвиге токов равном При
При изменении тока обмотки AX от нуля до Im магнитный поток прямого поля будет изменяться от Таким образом, в обоих случаях при изменении амплитуды одного из токов результирующее магнитное поле будет эллиптическим, представленным суммой двух круговых вращающихся магнитных полей с неравными магнитными потоками.
|

 Рис. 6.1
Рис. 6.1

 ,
,  ,
,  .
.
 ,
, 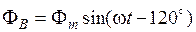 ,
,  .
. . Его абсолютное значение
. Его абсолютное значение 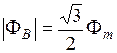 .
.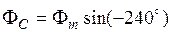 . Его абсолютное значение
. Его абсолютное значение  .
.
 ,
,




 ,
,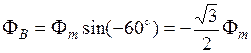 ,
, .
.
 .
.
 , где n 1 – частота вращения поля в оборотах в минуту, f – частота тока, герц, p – число пар полюсов поля.
, где n 1 – частота вращения поля в оборотах в минуту, f – частота тока, герц, p – число пар полюсов поля. (об/мин), где p – число пар полюсов машины или число периодов укладки обмотки в пазах статора.
(об/мин), где p – число пар полюсов машины или число периодов укладки обмотки в пазах статора.

 .
. .
. и
и  .
.
 .
.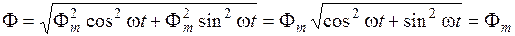 .
. или W = w.
или W = w. и
и  .
.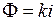 , тогда
, тогда  и
и  .
.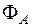 - с мнимой осью комплексной плоскости. Вектор результирующего магнитного потока
- с мнимой осью комплексной плоскости. Вектор результирующего магнитного потока 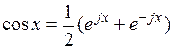 и
и  ,
, или, учитывая, что
или, учитывая, что  ,
,



 ;
; ,
,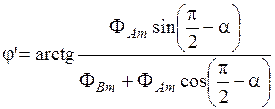 ;
; ,
, .
. или
или  .
. и
и  , тогда
, тогда 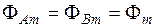 ,
,  ,
,  и
и  .
. , тогда
, тогда 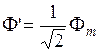 ,
,  ,
,  ,
,  .
.
 .
. раз больше амплитуды магнитного потока отдельной рамки, а направление магнитного потока равно 45 ° в пространстве.
раз больше амплитуды магнитного потока отдельной рамки, а направление магнитного потока равно 45 ° в пространстве. и обратного поля
и обратного поля  , при этом
, при этом  .
.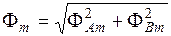 .
.
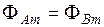 , тогда
, тогда
 ;
;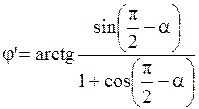 ;
;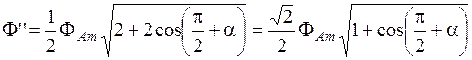 ;
; .
.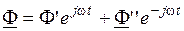 может быть представлен суммой двух вращающихся магнитных полей. Первое поле, представленное магнитным потоком
может быть представлен суммой двух вращающихся магнитных полей. Первое поле, представленное магнитным потоком  вращается против часовой стрелки на комплексной плоскости, и второе поле, представленное магнитным потоком
вращается против часовой стрелки на комплексной плоскости, и второе поле, представленное магнитным потоком  , вращается на комплексной плоскости с частотой w по часовой стрелке.
, вращается на комплексной плоскости с частотой w по часовой стрелке. магнитный поток прямого поля изменяется от
магнитный поток прямого поля изменяется от  до величины
до величины  .
. при a = 0 до нуля при
при a = 0 до нуля при  .
. приводит к увеличению магнитного потока прямого поля от
приводит к увеличению магнитного потока прямого поля от 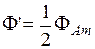 до
до  и к уменьшению магнитного потока обратного поля от
и к уменьшению магнитного потока обратного поля от  до нуля. При изменении a от нуля
до нуля. При изменении a от нуля  будет усиливаться обратное магнитное поле, а прямое поле будет уменьшаться.
будет усиливаться обратное магнитное поле, а прямое поле будет уменьшаться.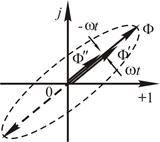 Рис. 6.9
Рис. 6.9
 ;
; .
.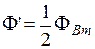 до
до  . Магнитный поток обратного поля будет в этом случае изменяться от
. Магнитный поток обратного поля будет в этом случае изменяться от  до
до  , при
, при  магнитный поток обратного магнитного поля будет равен нулю.
магнитный поток обратного магнитного поля будет равен нулю.


