Обобщенный метод наименьших квадратов (ОМНК)
При нарушении гомоскедастичности и наличии автокорреляции ошибок рекомендуется традиционный метод наименьших квадратов (известный в английской терминологии как метод OLS – Ordinary Least Squares) заменять обобщенным методом, т.е. методом GLS (Generalized Least Squares). Обобщенный метод наименьших квадратов применяется к преобразованным данным и позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии. Остановимся на использовании ОМНК для корректировки гетероскедастичности. Как и раньше, будем предполагать, что среднее значение остаточных величин равно нулю. А вот дисперсия их не остается неизменной для разных значений фактора, а пропорциональна величине
где При этом предполагается, что В общем виде для уравнения Иными словами, от регрессии
а исходные данные для данного уравнения будут иметь вид:
По отношению к обычной регрессии уравнение с новыми, преобразованными переменными представляет собой взвешенную регрессию, в которой переменные Оценка параметров нового уравнения с преобразованными переменными приводит к взвешенному методу наименьших квадратов, для которого необходимо минимизировать сумму квадратов отклонений вида
Соответственно получим следующую систему нормальных уравнений:
Если преобразованные переменные
При обычном применении метода наименьших квадратов к уравнению линейной регрессии для переменных в отклонениях от средних уровней коэффициент регрессии
Как видим, при использовании обобщенного МНК с целью корректировки гетероскедастичности коэффициент регрессии Аналогичный подход возможен не только для уравнения парной, но и для множественной регрессии. Предположим, что рассматривается модель вида
для которой дисперсия остаточных величин оказалась пропорциональна
рассматриваемая модель примет вид
где ошибки гетероскедастичны. Для того чтобы получить уравнение, где остатки
Это уравнение не содержит свободного члена. Вместе с тем, найдя переменные в новом преобразованном виде и применяя обычный МНК к ним, получим иную спецификацию модели:
Параметры такой модели зависят от концепции, принятой для коэффициента пропорциональности
предположить, что
Применение в этом случае обобщенного МНК приводит к тому, что наблюдения с меньшими значениями преобразованных переменных Пример. Пусть
является моделью издержек производства с объемными факторами. Предполагая, что
где параметры Если предположить, что в модели с первоначальными переменными дисперсия остатков пропорциональна квадрату объема продукции,
В нем новые переменные: Гипотеза о пропорциональности остатков величине фактора может иметь реальное основание: при обработке недостаточно однородной совокупности, включающей как крупные, так и мелкие предприятия, большим объемным значениям фактора может соответствовать большая дисперсия результативного признака и большая дисперсия остаточных величин. При наличии одной объясняющей переменной гипотеза
в уравнение
в котором параметры Пример. Рассматривая зависимость сбережений
Применяя обобщенный МНК к данной модели в предположении, что ошибки пропорциональны доходу, было получено уравнение для преобразованных данных:
Коэффициент регрессии первого уравнения сравнивают со свободным членом второго уравнения, т.е. 0, 1178 и 0, 1026 – оценки параметра Переход к относительным величинам существенно снижает вариацию фактора и соответственно уменьшает дисперсию ошибки. Он представляет собой наиболее простой случай учета гетероскедастичности в регрессионных моделях с помощью обобщенного МНК. Процесс перехода к относительным величинам может быть осложнен выдвижением иных гипотез о пропорциональности ошибок относительно включенных в модель факторов. Использование той или иной гипотезы предполагает специальные исследования остаточных величин для соответствующих регрессионных моделей. Применение обобщенного МНК позволяет получить оценки параметров модели, обладающие меньшей дисперсией.
|

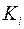 , т.е.
, т.е. ,
, – дисперсия ошибки при конкретном
– дисперсия ошибки при конкретном  -м значении фактора;
-м значении фактора; 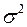 – постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков;
– постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков;  при
при 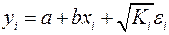 . В ней остаточные величины гетероскедастичны. Предполагая в них отсутствие автокорреляции, можно перейти к уравнению с гомоскедастичными остатками, поделив все переменные, зафиксированные в ходе
. В ней остаточные величины гетероскедастичны. Предполагая в них отсутствие автокорреляции, можно перейти к уравнению с гомоскедастичными остатками, поделив все переменные, зафиксированные в ходе  . Тогда дисперсия остатков будет величиной постоянной, т. е.
. Тогда дисперсия остатков будет величиной постоянной, т. е.  .
. по
по 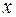 мы перейдем к регрессии на новых переменных:
мы перейдем к регрессии на новых переменных:  и
и  . Уравнение регрессии примет вид:
. Уравнение регрессии примет вид: ,
, ,
,  .
.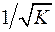 .
.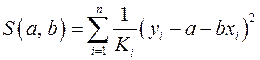 .
.
 можно определить как
можно определить как .
.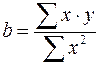 .
. .
. ,
,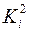 .
.  и
и  . Ввиду того, что
. Ввиду того, что ,
, ,
,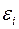 гомоскедастичны, перейдем к новым преобразованным переменным, разделив все члены исходного уравнения на коэффициент пропорциональности
гомоскедастичны, перейдем к новым преобразованным переменным, разделив все члены исходного уравнения на коэффициент пропорциональности  . Уравнение с преобразованными переменными составит
. Уравнение с преобразованными переменными составит .
.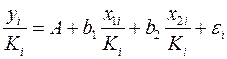 .
.
 , т.е.
, т.е.  и
и  , то обобщенный МНК предполагает оценку параметров следующего трансформированного уравнения:
, то обобщенный МНК предполагает оценку параметров следующего трансформированного уравнения: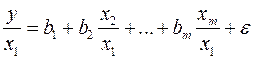 .
. имеют при определении параметров регрессии относительно больший вес, чем с первоначальными переменными. Вместе с тем, следует иметь в виду, что новые преобразованные переменные получают новое экономическое содержание и их регрессия имеет иной смысл, чем регрессия по исходным данным.
имеют при определении параметров регрессии относительно больший вес, чем с первоначальными переменными. Вместе с тем, следует иметь в виду, что новые преобразованные переменные получают новое экономическое содержание и их регрессия имеет иной смысл, чем регрессия по исходным данным. – численность работников, тогда уравнение
– численность работников, тогда уравнение
 , а в качестве факторов следующие показатели: производительность труда
, а в качестве факторов следующие показатели: производительность труда  и фондовооруженность труда
и фондовооруженность труда  . Соответственно трансформированная модель примет вид
. Соответственно трансформированная модель примет вид ,
, ,
,  ,
,  численно не совпадают с аналогичными параметрами предыдущей модели. Кроме этого, коэффициенты регрессии меняют экономическое содержание: из показателей силы связи, характеризующих среднее абсолютное изменение издержек производства с изменением абсолютной величины соответствующего фактора на единицу, они фиксируют при обобщенном МНК среднее изменение затрат на работника; с изменением производительности труда на единицу при неизменном уровне фовдовооруженности труда; и с изменением фондовооруженности труда на единицу при неизменном уровне производительности труда.
численно не совпадают с аналогичными параметрами предыдущей модели. Кроме этого, коэффициенты регрессии меняют экономическое содержание: из показателей силы связи, характеризующих среднее абсолютное изменение издержек производства с изменением абсолютной величины соответствующего фактора на единицу, они фиксируют при обобщенном МНК среднее изменение затрат на работника; с изменением производительности труда на единицу при неизменном уровне фовдовооруженности труда; и с изменением фондовооруженности труда на единицу при неизменном уровне производительности труда. , можно перейти к уравнению регрессии вида
, можно перейти к уравнению регрессии вида .
. – затраты на единицу (или на 1 руб. продукции),
– затраты на единицу (или на 1 руб. продукции), 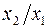 – фондоемкость продукции,
– фондоемкость продукции,  – трудоемкость продукции.
– трудоемкость продукции. трансформирует линейное уравнение
трансформирует линейное уравнение
 ,
, и
и  .
. .
.


