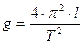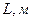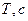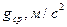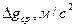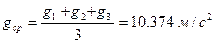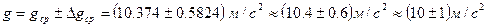маятника
Колебания математического Ученик 101 класса Куспиц Владислав 12 декабря 2010г.
Цель работы: изучить гармонические колебания на примере колебаний математического маятника, проверить экспериментально зависимость периода его колебания от длины и определить с помощью него ускорение свободного падения.
Оборудование: математический маятник, представляющий собой груз, подвешенный на тонкой длинной нити.
Схема установки:
Теоретическое положение:
Рассмотрим колебания математического маятника, представляющего собой небольшое массивное тело, подвешенное на столь длинной нити, что размерами тела по сравнению с длинной нити можно пренебречь, а массу тела считать сосредоточенной в точке. Ясно, что если заставить груз качаться, то движение этого груза будет колебательным, но нет никакой уверенности, что удовлетворяется главное требование На рисунке показаны силы, действующие на груз маятника, выведенного из положения равновесия. Сила тяжести разбита на две составляющие: радикальную, направленную вдоль нити, и тангенциальную, направленную по касательной к линии движения. Тангенциальная составляющая направлена в сторону положения равновесия, она стремиться восстановить это положение. Поэтому её часто называют возвращающей силой:
Однако для малых углов
Теперь закон изменения силы имеет вид:
Поэтому период колебаний маятника при малых углах отклонения:
Из формулы следует, что период колебаний маятника не зависит от массы груза. Поэтому для данного положения на Земле и, таким образом, для определённого значения g, период зависит только от длины подвеса L. В частности, в той степени, в какой справедливо приближение Описание лабораторной установки: Маятник представляет собой гирьку, подвешенную на длинной тонкой нити. За длину маятника принимается расстояние от точки подвеса до центра шарика. Свободный конец нити зажат в подвесе, закреплённом в зажиме штатива. Время качаний определяется секундомером. Рассмотрим несколько случаев: 1) Проверим зависимость периода колебаний маятника от значения амплитуды А при неизменных массе грузов m и длине L. 2) Проверим зависимость периода колебаний маятника от значения длины маятника L при неизменных массе грузов m и такой амплитуде L, что период колебаний от неё не зависит. 3) Проверим зависимость периода колебаний маятника от массы подвешенного груза m при неизменных дине маятника L и значения амплитуды А.
Обработка результатов: 1) Среднее значение периода колебаний рассчитаем по формуле:
Погрешность результатов рассчитаем по формуле:
2) При проверке независимости периода колебаний маятника от значения амплитуды, находится такая величина
Это значит, что при амплитуде колебаний, большей чем
Запишем полученные результаты в Таблицу 1:
Вывод: при малых углах отклонения груза от положения равновесия, период колебаний остаётся постоянным.
Запишем результаты в Таблицу 2:
Вывод: период колебаний маятника зависит от его длины, чем она больше, тем больше и период колебаний.
Проверим независимость периода колебаний маятника от массы подвешенного груза.
Запишем полученные результаты в Таблицу 3:
Вывод: период колебаний не зависит от массы подвешенного груза. С помощью таблицы 2 определим ускорение свободного падения
Окончательный ответ:
Вывод по работе: В ходе работы было выяснено, что период колебания математического маятника не зависит от амплитуды (при малых углах) и массы подвешенного груза, но зависит от длины маятника. Так же с помощью маятника было определено ускорение свободного падения.
|


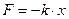 , то есть что колебание будет гармоническим.
, то есть что колебание будет гармоническим.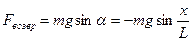
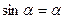 , и в этом случае
, и в этом случае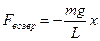
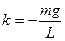
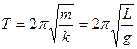
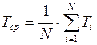
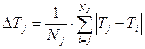
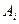 , при которой выполняется соотношение:
, при которой выполняется соотношение: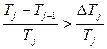
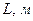
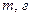
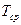
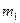
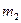
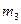
 . Для этого воспользуемся формулой:
. Для этого воспользуемся формулой: