Магнитные моменты атомов
По модели атома Бора электроны вращаются вокруг ядер по некоторым орбитам (рис.17.17). Предположим, что эти орбиты - круговые с радиусом 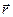 . .
Рис.17.17.Атом как элементарный магнитный диполь
Орбитальный механический момент (орбитальный момент импульса) такого электрона равен
Здесь
- эффективный электрический ток – элементарный ток, созданный движущимся вокруг ядра электроном, Т - период вращения электрона, v - скорость движения электрона по орбите, е - элементарный заряд. Отношение магнитного дипольного момента к механическому моменту называется гиромагнитным отношением. Орбитальное гиромагнитное отношение равно:
Квантовая теория доказывает, что момент импульса любой частицы - как орбитальный, так и собственный, квантуется. Величина
является естественной единицей момента импульса. Орбитальный механический момент электрона равен
Здесь Собственный механический момент (спин) электрона равен
где s – спиновое квантовое число ( для электрона s= 1/2). Орбитальный магнитный момент электрона равен
Собственный магнитный момент электрона равен
где Величина
называется магнетоном Бора. Полный магнитный момент атомов определяется суммой собственных и орбитальных магнитных моментов электронов, входящих в состав атома. Собственный магнитный момент атомов определяется суммой собственных магнитных моментов электронов, входящих в состав атома. Для разных веществ собственный магнитный момент атомов разный, но всегда кратен целому числу магнетонов Бора. У металлов в твердом состоянии часть электронов коллективизируется - то есть отрывается от "своих" атомов и, следовательно, суммироваться должны только те электроны, которые остались на ионе. Для некоторых веществ магнитный момент атомов равен нулю, для других - не равен. Причем так оказывается, что, например, медь в атомарном (газообразном) состоянии имеет магнитный момент, равный одному магнетону Бора, а в твердом состоянии собственный магнитный момент атомов (точнее - ионов) равен нулю.
17.3.2.Магнитный диполь во внешнем однородном Представим магнитный диполь в виде рамки с током (рис. 17.18).
Рис. 17.18. Магнитный диполь во внешнем поле На элементы тока
Тогда: dF 1 = dF 3 = 0, так как dF 2 = dF 4 = Параллельные и противоположно направленные силы dF 2 и dF 4 образуют пару сил, момент которой равен dM = dF × a = Тогда суммарный момент, действующий на рамку, равен M = I × b × B × a = I × B × S = Pm × B, (17.40) где S = a × b – площадь рамки. В векторной форме момент равен
Равновесие для диполя в магнитном поле наступает, когда момент пары сил равен нулю:
На нижерасположенном рисунке показано вращение рамки с током («магнитного диполя») в однородном магнитном поле под действием вращающего момента  из произвольного положения ( из произвольного положения ( ) в положение устойчивого равновесия ( ) в положение устойчивого равновесия ( ). ).
|


 (17.28)
(17.28) Орбитальный магнитный момент такого электрона равен
Орбитальный магнитный момент такого электрона равен (17.29)
(17.29) (17.30)
(17.30) (17.31)
(17.31)
 .(17.32)
.(17.32) - орбитальное квантовое число (
- орбитальное квантовое число ( = 0,1,2,3,…(n- 1), где n – главное квантовое число).
= 0,1,2,3,…(n- 1), где n – главное квантовое число).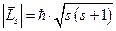 ,(17.33)
,(17.33) Дж/Т(17.34)
Дж/Т(17.34) Дж/Т, (17.35)
Дж/Т, (17.35) - спиновое гиромагнитное отношение.
- спиновое гиромагнитное отношение.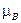 =
=  (17.36)
(17.36)

 действуют магнитные силы (силы Ампера)
действуют магнитные силы (силы Ампера) .(17.37)
.(17.37) ;
; .(17.38)
.(17.38)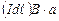 .(17.39)
.(17.39) .(17.41)
.(17.41)




