Использование законов распределения случайных величин при имитации экономических процессов

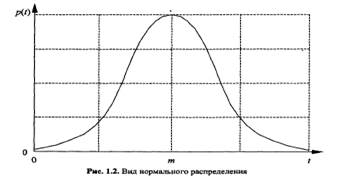
Нормальное распределение.

Нормальное, или гауссово распределение, - это, несомненно, одно из наиболее важных и часто используемых видов непрерывных распределений. Оно симметрично относительно математического ожидания.

Важный показатель для характеристики распределения – это ассиметрия, то есть отклонение наиболее вероятной величины от среднего значения.

Часто эксцесс интерпретируется как «крутизна» распределения, но это неточно и неполно. График распределения может выглядеть сколь угодно крутым в зависимости от силы вариации признака: чем слабее вариация, тем круче кривая распределения при данном масштабе. Не говоря уже о том, что, изменяя масштабы по оси абсцисс и по оси ординат, любое распределение можно искусствен но сделать «крутым» и «пологим». Чтобы показать, в чем состоит эксцесс распределения, и правильно его интерпретировать, нужно сравнить ряды с одинаковой силой вариации (одной и той же величиной?) и разными показателями эксцесса. Чтобы не смешать эксцесс с асимметрией, все сравниваемые ряды должны быть симметричными. Такое сравнение изображено на рис. 5.4.

Экспоненциальное (пуассоновское) распределение. Оно также занимает очень важное место при проведении системного анализа экономической деятельности. Этому закону распределения подчиняются многие явления, например:

• время поступления заказа на предприятие;

• посещение покупателями магазина-супермаркета;

• телефонные разговоры;

• срок службы деталей и узлов в компьютере, установленном, например, в бухгалтерии.

 

 

Равномерное распределение на интервале (0,1). Все значения имеют одинаковую вероятность. Такое распределение называют еще плоское.

Равномерное распределение на произвольном интервале, получается умножением равномерного на произвольное число.

 

 

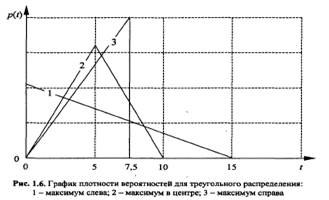
Треугольное распределение – аналог нормального или пуассоновского, но для дискретных событий, то есть когда у системы может быть только 2-3 состояния с легко просчитываемой вероятностью.

 

Дискретное распределение (общий случай). Так же как и равномерное на произвольном интервале, но вероятности присвоены только целым значениям.