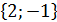Контрольная работа № 1. Факультет Институт заочного обучения
ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ» Kафедра «Математика-1»
Факультет Институт заочного обучения
Направление подготовки: [080100] Экономика (бакалавры)
КОНТРОЛЬНАЯ РАБОТА № 1
по дисциплине «Линейная алгебра» Вариант № 7
Студентка: Кравченко Анастасия Александровна Курс 1 № группы: ЗБ3-ЭФ 1-9с Номер зачетной книжки: 143147 Преподаватель: профессор Калачев Н.В.
2014г Таблица оценок
ВАРИАНТ 7 Контрольная работа № 1
1. Даны матрицы
Найти ранг матрицы 2. Методом обратной матрицы решить систему:
3. Установить, имеет ли однородная система
ненулевое решение. Найти общее решение системы. 4. Найти значение параметра α, при котором векторы 5. Даны четыре вектора
в некотором базисе. Показать, что векторы 6. Найти собственные значения и собственные векторы линейного оператора 7. а) Методом Лагранжа привести квадратичную форму f (x 1, x 2)=4 x 12+3 x 22+4 x 1 x 2
к каноническому виду (указать пример соответствующего преобразования координат). б) По критерию Сильвестра исследовать на знакоопределенность квадратичную форму f (x 1, x 2, x 3)= – 2 x 12 + 5 x 22 + 3 x 32 +2 x 1 x 2 – 2 x 1 x 3 – 2 x 2 x 3.
1. Даны матрицы
Найти ранг матрицы C=A∙B.
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12)
1. Вычесть из 2й строки 1ю.
2. Домножаем 1ю строку на
3. Меняем 2ю и 3ю строки местами.
Количество линейно независимых строк = 3
Ответ: Ранг матрицы = 3.
2. Методом обратной матрицы решить систему:
Находим определитель матрицы.
Определяем матрицу миноров матрицы А.
1)
2)
3)
4)
5)
6)
7)
8)
9)
Меняем знаки у выделенных элементов, получаем:
Ответ: X=1; Y=2; Z=1.
3. Установить, имеет ли однородная система
ненулевое решение. Найти общее решение системы.
Преобразовываем матрицу до того момента, пока все показатели, находящиеся ниже диагонали, не будут = 0.
Из 2й строки вычитаем 1ю, получаем:
Из 3й строки вычитаем 1ю, получаем:
Из 4й строки вычитаем 1ю, получаем:
Умножаем 3ю строку на -1, получаем:
Из 3й строки вычитаем 2ю, далее меняем местами 3ю и 4ю строки, получаем:
Делим 3ю строку на 2, далее умножаем на -1, вычитаем из 3й строки 2ю, получаем:
Делим 2ю строку на 2, получаем систему:
4. Найти значение параметра α, при котором векторы
5. Даны четыре вектора
в некотором базисе. Показать, что векторы
Показатели линейно независимы
Далее необходимо найти обратную матрицу Вычисляем матрицу миноров матрицы A.
1) 2) 3) 4) 5) 6) 7) 8) 9)
У выделенных элементов меняем знаки на противоположные.
1) 2) 3)
6. Найти собственные значения и собственные векторы линейного оператора
Находим собственные значения:
Далее для каждого собственного значения найдем его собственные векторы.
Решаем систему
Необходимо подобрать значение Пусть
Таким образом, собственные векторы собственного значения
Необходимо подобрать значение Пусть
Таким образом, собственные векторы собственного значения 7. а) Методом Лагранжа привести квадратичную форму f (x 1, x 2)=4 x 12+3 x 22+4 x 1 x 2
к каноническому виду (указать пример соответствующего преобразования координат). б) По критерию Сильвестра исследовать на знакоопределенность квадратичную форму f (x 1, x 2, x 3)= – 2 x 12 + 5 x 22 + 3 x 32 +2 x 1 x 2 – 2 x 1 x 3 – 2 x 2 x 3.
|
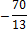
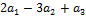
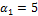
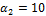
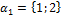
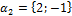
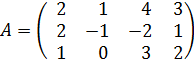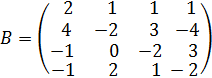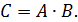
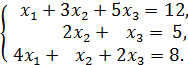
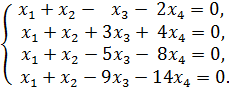
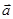и 
.
и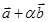 
перпендикулярны, если 
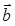= (– 1; – 3; 2).
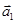=(2;1;0); 
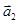=(1;–1;2); 
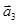=(2;2;–1); 
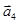=(3;7;– 7)
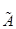, заданного матрицей А = 
.
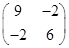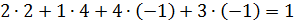
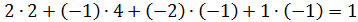
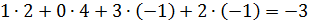
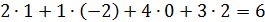
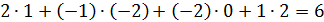
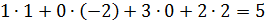
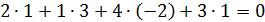
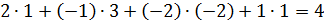
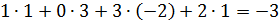
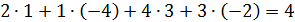
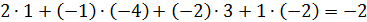
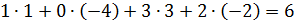
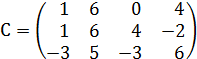
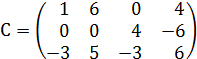
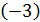и из 3й строки вычитаем 1ю.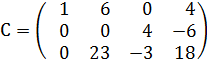
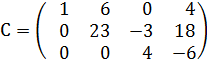
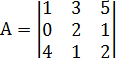
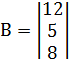
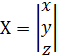
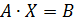
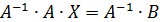
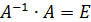
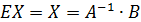
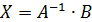
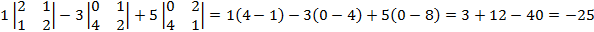
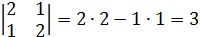
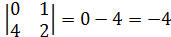
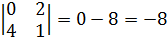
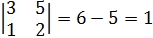
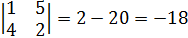
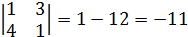
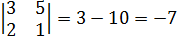
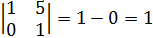
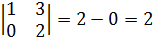
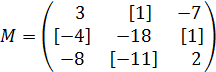
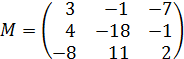
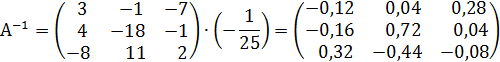
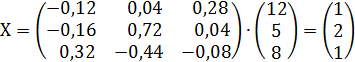
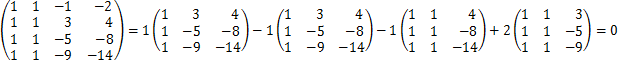
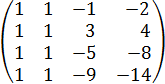
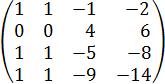
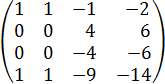
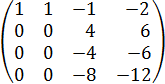
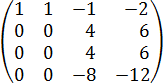
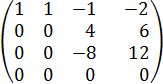
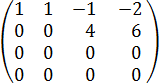
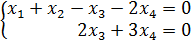
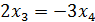
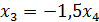
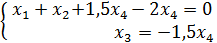
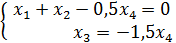
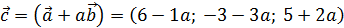
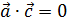
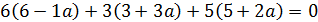
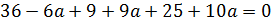
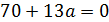
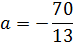
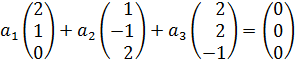
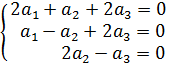
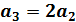
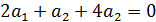
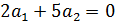
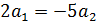
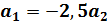
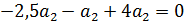
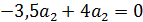
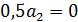
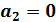
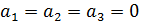следовательно образуют базис.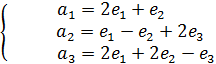
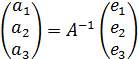
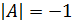(определитель матрицы).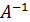
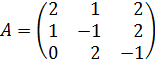
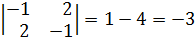
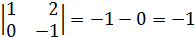
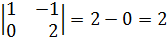
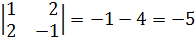
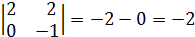
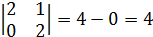
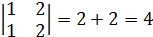
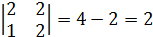
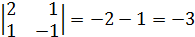
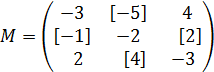
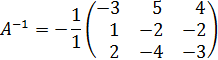
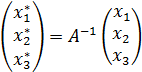
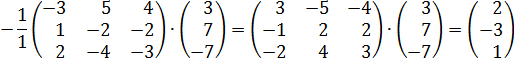
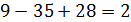
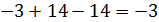
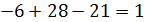
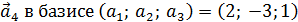
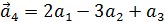
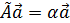
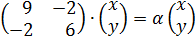
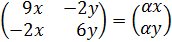
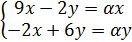
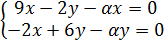
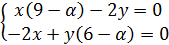
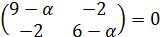
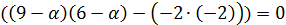
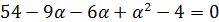
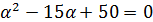
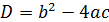
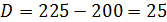
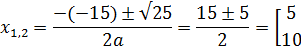
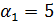
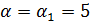
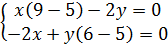
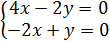
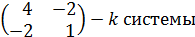
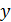так, чтобы 
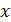было целым и положительным числом.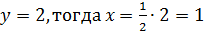
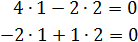
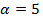представляют собой координаты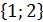 
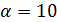
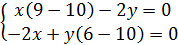
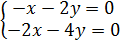
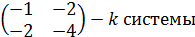
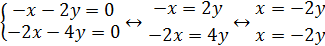
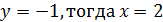
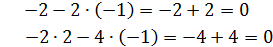
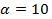представляют собой координаты 
