Краткие теоретические сведения
Лабораторная работа 2. Изучение электропроводности биологических объектов с использованием специализированного аппаратно-программного комплекса с удаленным доступом
Биологическим объектам присущи пассивные электрические свойства: сопротивление и емкость. Биологические ткани и клетки обладают свойствами как проводников, так и диэлектриков. Проводимость этих объектов обусловливается наличием свободных ионов. Диэлектрические свойства биологических объектов и величина диэлектрической проницаемости определяются структурными компонентами и явлениями поляризации. Общей особенностью биообъектов является несоответствие между большим содержанием электролитов в клетках живых организмов и низкими величинами их электропроводности. Экспериментально определяя сопротивление живых клеток и тканей, следует учитывать их чувствительность к действию электрического тока. При этом используют малые напряжения, чтобы не нарушать целостности образца. Электропроводность клеток и тканей для постоянного тока Электропроводность L – это величина, обратная сопротивлению R проводника:
где r – удельное сопротивление, l – длина проводника, S – сечение проводника. Сопротивление R является коэффициентом пропорциональности между разностью потенциалов V и силой тока I:
При пропускании постоянного тока через живые ткани было установлено, что сила тока не остается постоянной во времени, хотя прикладываемое напряжение не изменяется. Сразу после подключения источника напряжения сила тока начинает непрерывно падать и устанавливается на уровне много ниже исходного (рис. 5.10).
Рис. 5.10. Изменение силы тока во времени при наложении на ткань постоянной разности потенциалов: а) отсутствие поляризации, б) наличие поляризации [1]. Это происходит из-за возникновения в образце электродвижущей силы противоположного направления – ЭДС поляризации P(t). При отключении образца от источника напряжения в цепи некоторое время будет наблюдаться ток обратного направления, вызванный этой ЭДС. Таким образом, закон Ома для такого случая записывают как:
Остановимся на объяснении явления поляризации биологической ткани чуть подробнее. Т. к. любой биологический объект имеет сложную организацию, влияние электрического поля и реакция на него будут различными на разных структурных уровнях. Рассмотрим процессы, происходящие в биологических тканях при приложении внешнего электрического поля. 1. Как известно, электрическое поле вызывает упорядоченное движение свободных зарядов, в нашем случае – ионов. Следовательно, возникает электрический ток, что приводит, согласно закону Джоуля-Ленца, к выделению тепла. Этот процесс дает вклад в активную составляющую импеданса. 2. Также электрическое поле действует на связанные электрические заряды, не имеющие возможности свободного перемещения и на заряды, перемещение которых возможно лишь в малой ограниченной области. Однако воздействие на эти обе группы зарядов приводит к значительному эффекту – перераспределению в пространстве электрических зарядов или, другими словами, поляризации биологической ткани. Поляризация по своей природе делится на несколько видов: 1. Электронная поляризация - это смещение электронов на своих орбитах относительно положительно заряженных ядер, что приводит к возникновению индуцированных, наведенных диполей. Время возникновения электронной поляризации после мгновенного наложения поля, называемое временем релаксации, равняется 10-16-10-14 с. Возникающий диполь имеет небольшую величину. 2. Ионная поляризация – это смещение иона относительно кристаллической решетки, что также приводит к возникновению дипольного момента. Характерное время релаксации - 10-14-10-12 с. 3. Дипольная (ориентационная) поляризация появляется вследствие ориентации полярных молекул в составе вещества в соответствии с направлением электрического поля. Имеет большое значение для таких полярных молекул как вода, спирты, белковые макромолекулы с диссоциированными группами и т.п. Время релаксации для данного типа поляризации совпадает со временем поворота молекул, а потому зависит от вязкости среды, температуры и радиуса молекул. В зависимости от указанных факторов это время изменяется в пределах 10-13-10-7 с. 4. Макроструктурная поляризация возникает вследствие неоднородности электрических свойств вещества. При наличии слоев с различной электропроводностью после наложения электрического поля заряды двигаются до границы проводящего слоя и там накапливаются. В результате этого процесса проводящая часть ткани приобретает дипольный момент и ведет себя подобно гигантской поляризационной молекуле. Время релаксации этого типа - 10-8-10-3 с. 5. Поверхностная поляризация происходит на поверхностях, имеющих двойной электрический слой. При наложении поля происходит перераспределение ионов диффузионной части двойного электрического слоя: частицы дисперсной фазы смещаются в одну сторону, а ионы диффузионного слоя – в другую, таким образом формируя наведенные диполи. Время релаксации поверхностной поляризации от 10-16 до 10-14 с. 6. Электролитическая поляризация возникает между электродами, опущенными в раствор электролита, при пропускании через них электрического тока. При наложении разности потенциалов на электроды происходит перераспределение потенциалопределяющих ионов в диффузионной части двойного электрического слоя: в области катода концентрация ионов (катионов) увеличится, а в области анода – уменьшится. В процессе дальнейшего изменения концентрации ионов в приэлектродных слоях могут начаться электрохимические реакции на электродах: ионы будут переходить из раствора на один электрод, а с другого электрода уходить в раствор. Таким образом, и в случае электролитической поляризации появление ЭДС поляризации обусловлено смещением зарядов, которое в данном случае проявляется как изменение концентрации ионов в приэлектродной зоне. Время релаксации данного типа поляризации измеряется величинами порядка 10-4-102 с. Различают также несколько структурных уровней поляризации: 1. В макроскопических областях, ограниченных средами с низкой электропроводностью, под действием электрического поля происходит перемещение ионов межклеточной жидкости до границ области. Возникает большой дипольный момент, величина которого определяется размерами области и суммарным зарядом перемещенных ионов. 2. В пределах отдельной клетки происходит смещение ионов цитозоли до границ клеточной мембраны, имеющей низкую электропроводность. Дипольный момент отдельной клетки невелик ( 3. Для ядер клеток и других внутриклеточных структур, имеющих собственную мембрану, механизм поляризации аналогичен клеточному. Дипольный момент мал по сравнению с клеточным. 4. Ориентационная поляризация белков и других макромолекул. Величина поляризации зависит от состояния этих молекул (свободные или связанные). 5. Ориентационная поляризация воды и электролитов. Величина поляризации наименьшая из всех.
Схематически разные структурные уровни поляризации представлены на рис. 5.11.
Рис. 5.11. Структурные уровни поляризации биологической ткани
Помимо прямого исследования зависимости поляризации от частоты, существует интегральный способ оценки этой зависимости – определение изменения поляризации во времени в ответ на ступенчатое (мгновенное) включение внешнего электрического поля. Если в момент времени t = 0 напряженность внешнего электрического поля возрастает от нуля до значения
где Таблица 5.2. Значения времени релаксации для разных типов поляризации
В постоянном электрическом поле проявляются все типы поляризации и величина диэлектрической проницаемости максимальна.
Электропроводность клеток и тканей для переменного тока Как известно, переменный ток – это ток, который изменяется как по величине, так и по направлению. Далее мы будем рассматривать только такие токи, которые подчиняются гармоническому закону:
где При прохождении через ткани переменного тока, изменяющегося по гармоническому закону, падение напряжения на биологической ткани также изменяется по закону
В общем случае амплитудные значения силы тока
И если переписать предыдущее уравнение в виде:
то получим, что амплитудное значение тока
Величина
где а Однако, принято считать, что индуктивность биологических тканей пренебрежимо мала (
Сдвиг фаз
Т. о. напряжение отстает по фазе от тока ( Значения угла сдвига фаз, полученные при частоте 1 кГц для различных биологических объектов приведены в табл. 5.3.
Таблица 5.3 – Угол сдвига фаз между током и напряжением для различных биологичеких объектов
Итак, для биологического объекта импеданс носит составной (комплексный) характер Его активная составляющая Как известно, емкость является коэффициентом пропорциональности между зарядом и потенциалом и определяется как отношение изменения заряда проводника Dq к изменению его потенциала Dj:
Для плоского конденсатора она определяется по формуле:
где S – площадь пластин, d – расстояние между ними. Измеряемая емкость биологического объекта определяется поляризационной емкостью Cp, которая возникает в момент прохождения тока. Поляризационная емкость будет определяться следующим уравнением:
где в числителе задается изменение во времени заряда Dq, а в знаменателе – изменение потенциала Dj (I0 и It – начальное и конечное значение силы тока, I – ток мгновенный, R – сопротивление объекта). К поляризационной емкости биологического объекта добавляется значительная по величине статическая емкость мембран (1 мкФ/см2). Согласно последнему уравнению, величина поляризационной емкости зависит от времени действия поля, а значит на низких частотах может превышать величину статической емкости. На более высоких частотах (порядка 10 кГц) статическая емкость на несколько порядков выше поляризационной. А так как эти емкости соединены последовательно, то на высоких частотах общая величина емкости определяется меньшей по величине поляризационной емкостью. Абсолютная величина (модуль) электрического импеданса определяется выражением:
При этом как абсолютная величина импеданса Зависимость электрического импеданса от частоты носит название дисперсии импеданса. Наличие активных и реактивных свойств импеданса можно моделировать, используя эквивалентные электрические схемы. Рассмотрим некоторые из них (рис. 5.12).
Для схемы с последовательным соединением активного
Однако в области низких частот эта схема имеет существенное расхождение с экспериментальными данными: при При параллельном соединении активного
Полученное математическое выражение Наилучшее согласие с экспериментом обеспечивает эквивалентная схема, приведенная на рис. 5.12, в: на низких частотах величина импеданса определяется сопротивлением
Тогда видно, что в области низких частот, т. е. при
Как уже говорилось, и Рассмотрим для начала емкостные свойства. Величина емкостного (реактивного) сопротивления конденсатора описывается формулой Характеристикой реакции диэлектрической среды на электрическое поле является относительная диэлектрическая проницаемость Вектором поляризации
В изотропной среде вектор поляризации
где Отсюда легко видеть, что диэлектрическая проницаемость
Таким образом, именно зависимость поляризации среды При увеличении частоты переменного тока (электрического поля) промежуток времени действия электрического поля (≈1/2 периода) уменьшается. Если этот промежуток времени меньше времени релаксации Для оценки жизнеспособности ткани служит т. н. коэффициент поляризации: где Жизнеспособная ткань имеет Итак, при прохождении переменного тока различной частоты через живую ткань отмечается явление дисперсии электропроводности, когда при повышении частоты тока сопротивление живой ткани уменьшается до некоторой предельной величины. Это явление обусловлено гетерогенностью клеточных структур и веществ цитоплазмы, а также структурированной организацией клетки. При действии внешнего электрического поля происходит ориентация всех заряженных частиц, молекул, ионов и диполей, а также структур с индуцированным зарядом против поля. Ионы при перемещении по полю накапливаются на внутренних и клеточной мембранах. Все эти факторы создают реактивное (в нашем случае емкостное) сопротивление При изменении частоты тока происходит перезарядка мембран, переориентация молекул (т. е. поляризация). Поскольку у молекул и структур различные размеры и величины зарядов, то они имеют различное время релаксации
|

 ,
,

 .
. ), но при значительной плотности клеток их суммарный дипольный момент сравним по величине с дипольным моментом ткани.
), но при значительной плотности клеток их суммарный дипольный момент сравним по величине с дипольным моментом ткани.
 , то зависимость от времени поляризации
, то зависимость от времени поляризации  имеет одинаковый характер для всех механизмов:
имеет одинаковый характер для всех механизмов: ,
, – наибольшее значение поляризации и
– наибольшее значение поляризации и  – время релаксации.
– время релаксации. , с.
, с.
 – мгновенное значение силы тока в момент времени
– мгновенное значение силы тока в момент времени  ;
;  – амплитуда тока;
– амплитуда тока;  – циклическая частота колебаний.
– циклическая частота колебаний.
 и фазовый
и фазовый  сдвиг между напряжением и током
сдвиг между напряжением и током  определяются параметрами биологической ткани.
определяются параметрами биологической ткани. и напряжения
и напряжения 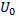 в цепи переменного тока связаны как
в цепи переменного тока связаны как

 и так на зываемым полным сопротивлением цепи или импедансом
и так на зываемым полным сопротивлением цепи или импедансом  :
:
 называется реактивным сопротивлением. Причем, как известно, реактивное сопротивление есть разность индуктивного
называется реактивным сопротивлением. Причем, как известно, реактивное сопротивление есть разность индуктивного  и емкостного
и емкостного  сопротивлений цепи:
сопротивлений цепи: ,
,

 ) а значит
) а значит
 между током
между током  и напряжением
и напряжением  можно вычислить из выражения:
можно вычислить из выражения: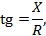

 ), а величина фазового сдвига
), а величина фазового сдвига 
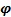 , град.
, град.
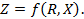
 связана, в первую очередь, с проводимостью внутренних жидких сред, являющихся электролитами. Различные процессы в тканях, сопровождающиеся необратимыми потерями энергии, также дают вклад в величину активной составляющей импеданса. Реактивная компонента
связана, в первую очередь, с проводимостью внутренних жидких сред, являющихся электролитами. Различные процессы в тканях, сопровождающиеся необратимыми потерями энергии, также дают вклад в величину активной составляющей импеданса. Реактивная компонента 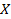 определяется емкостными свойствами исследуемой ткани, в частности, емкостью биологических мембран. Кроме того, в емкостную составляющую импеданса дает вклад и область контакта стимулирующих электродов с биологическими тканями.
определяется емкостными свойствами исследуемой ткани, в частности, емкостью биологических мембран. Кроме того, в емкостную составляющую импеданса дает вклад и область контакта стимулирующих электродов с биологическими тканями. .
. ,
, ,
,
 так и фазовый сдвиг
так и фазовый сдвиг 


 , что явно носит нефизический характер.
, что явно носит нефизический характер.
 удовлетворительно описывает частотную зависимость величины импеданса на низких частотах, но при
удовлетворительно описывает частотную зависимость величины импеданса на низких частотах, но при  , что не соответствует опытным данным
, что не соответствует опытным данным , на высоких частотах – параллельным соединением сопротивлений
, на высоких частотах – параллельным соединением сопротивлений 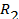 . Можно показать, что в этом случае
. Можно показать, что в этом случае
 , а в области высоких частот при
, а в области высоких частот при 



 : а – для эквивалентной схемы при различном соотношении активной и реактивной составляющих; б – экспериментальная зависимость для биологической ткани
: а – для эквивалентной схемы при различном соотношении активной и реактивной составляющих; б – экспериментальная зависимость для биологической ткани
 и
и  (а следовательно и
(а следовательно и  ), обладают свойством дисперсии. Вид кривой дисперсии импеданса (рис. 5.13, б) зависит от структурной целостности и от уровня обменных процессов.
), обладают свойством дисперсии. Вид кривой дисперсии импеданса (рис. 5.13, б) зависит от структурной целостности и от уровня обменных процессов. , а сама величина емкости для плоского конденсатора –
, а сама величина емкости для плоского конденсатора –  .
. – эта величина, определяющая, во сколько раз напряженность электростатического поля в данной точке среды меньше той напряженности электрического поля, которая возникла бы в вакууме при той же суперпозиции зарядов, создающих поле.
– эта величина, определяющая, во сколько раз напряженность электростатического поля в данной точке среды меньше той напряженности электрического поля, которая возникла бы в вакууме при той же суперпозиции зарядов, создающих поле. называется суммарный дипольный момент единицы объема среды
называется суммарный дипольный момент единицы объема среды  :
:
 параллелен вектору напряженности электрического поля
параллелен вектору напряженности электрического поля  и связан соотношением[С1]:
и связан соотношением[С1]:
 .
. и напряженностью поля E соотношением:
и напряженностью поля E соотношением:

 – значение импеданса на низкой частоте (обычно около 102 Гц);
– значение импеданса на низкой частоте (обычно около 102 Гц);  – на высокой частоте (>106 Гц).
– на высокой частоте (>106 Гц). , причем
, причем  тем больше, чем выше уровень обменных процессов и чем лучше сохранена структурная целостность данной ткани. При отмирании ткани ее
тем больше, чем выше уровень обменных процессов и чем лучше сохранена структурная целостность данной ткани. При отмирании ткани ее  . Поэтому с увеличением частоты тока
. Поэтому с увеличением частоты тока  часть из них (в первую очередь крупные частицы) не успевает переориентироваться и не участвует в создании внутренней ЭДС, вследствие чего ее величина уменьшается. В первом приближении эта теория удовлетворительно объясняет явление дисперсии электропроводности живой ткани, однако она не вскрывает причин изменения ее электропроводности при различных физиологических состояниях.
часть из них (в первую очередь крупные частицы) не успевает переориентироваться и не участвует в создании внутренней ЭДС, вследствие чего ее величина уменьшается. В первом приближении эта теория удовлетворительно объясняет явление дисперсии электропроводности живой ткани, однако она не вскрывает причин изменения ее электропроводности при различных физиологических состояниях.


