Криптография. Основные термины и определения. Условия стойкости (по Шеннону). Требования к криптографическим системам.
Криптография изучает методы преобразования информации, обеспечивающие ее конфиденциальность и аутентичность. Аутентичность информации - подлинность авторства и целостность. Алфавит - конечное множество используемых для кодирования информации знаков. Текст (сообщение) - упорядоченный набор из элементов алфавита. Зашифрование - процесс преобразования открытых данных в зашифрованные при помощи шифра. Вместо термина "открытые данные" часто употребляются термины открытый текст и исходный текст, а вместо "зашифрованные данные" - шифрованный текст. Расшифрование - процесс, обратный зашифрованию, т.е процесс преобразования зашифрованных данных в открытые при помощи ключа. В некоторых источниках отдельно выделяют термин дешифрование, подразумевая под этим восстановление исходного текста на основе шифрованного без знания ключа, то есть методами криптоанализа. Мы в дальнейшем будем считать расшифрование и дешифрование синонимами. Под шифрованием понимается процесс зашифрования или расшифрования. Также термин шифрование (в узком смысле) используется как синоним зашифрования. Однако неверно в качестве синонима шифрования использовать термин «кодирование» (а вместо «шифра» - «код»), так как под кодированием обычно понимают представление информации в виде знаков (букв алфавита). Криптографическая система, или шифр, представляет собой семейство Т обратимых преобразований открытого текста в шифрованный. Членам этого семейства можно взаимно однозначно сопоставить число К, называемое ключом. Преобразование Т определяется соответствующим алгоритмом и значением ключа К. Ключ — конкретное значение некоторых параметров алгоритма криптографического преобразования, обеспечивающее выбор одного преобразования из семейства. Секретность ключа должна обеспечивать невозможность восстановление исходного текста по шифрованному. Пространство ключей К - это набор возможных значений ключа. Обычно ключ представляет собой последовательный ряд букв алфавита. Следует отличать понятия ключ и пароль. Пароль также является секретной последовательностью букв алфавита, однако используется не для шифрования (как ключ), а для аутентификации субъектов. Гамма шифра – псевдослучайная двоичная последовательность, вырабатываемая по заданному алгоритму, для зашифрования открытых данных и расшифрования зашифрованных данных. Имитозащита – защита от навязывания ложных данных. Для обеспечения имитозащиты к зашифрованным данным добавляется имитовставка, представляющая собой последовательность данных фиксированной длины, полученную по определенному правилу из открытых данных и ключа.
Первое условие: для каждого допустимого сообщения T преобразования за- и расшифрования должны удовлетворять следующему свойству: T = D (E (T)). Второе условие, которому должен удовлетворять шифр, следующее: не должно существовать легко прослеживаемых связей между исходными и зашифрованными данными. Кроме того, шифр должен быть криптостойким, то есть устойчивым к попыткам дешифрования сообщений. Пусть возможна отправка сообщений T 1, T 2,..., Tn с вероятностью p 1, p 2,..., pn соответственно. Тогда мерой неопределенности сообщения для всех, кто обладает этой априорной информацией, может служить величина математического ожидания логарифма вероятности одного сообщения, взятая со знаком "минус":
Одной из важнейших характеристик качества шифра служит количество информации об исходном тексте, которое злоумышленник может извлечь из перехваченного шифротекста - оно находится как разность между априорной и апостериорной неопределенностью исходного сообщения: I = H (T) - H (T | T '). Эта величина всегда неотрицательна. Показателем здесь является, насколько уменьшится неопределенность исходного текста при получении соответствующего шифротекста по сравнению с априорной неопределенностью, и не станет ли она меньше допустимой величины. В наилучшем для разработчиков шифра случае обе эти неопределенности равны: H (T | T ') = H (T), то есть злоумышленник не может извлечь никакой полезной для себя информации об открытом тексте из перехваченного шифротекста: I = 0. Иными словами, знание шифротекста не позволяет уменьшить неопределенность соответствующего открытого текста, улучшить его оценку и увеличить вероятность его правильного определения. Шифры, удовлетворяющие данному условию, называются абсолютно стойкими или совершенными шифрами, так как зашифрованные с их применением сообщения не только не могут быть дешифрованы в принципе, но злоумышленник даже не сможет приблизиться к успешному определению исходного текста, то есть увеличить вероятность его правильного дешифрования. Условие стойкости (по Шеннону):Для того, чтобы шифр был абсолютно стойким, необходимо, чтобы неопределенность алгоритма шифрования была не меньше неопределенности шифруемого сообщения: H (E) Неопределенность алгоритма шифрования определяется точно так же, как и неопределенность сообщения - математическое ожидание двоичного логарифма вероятности использования алгоритма со знаком минус, - и имеет смысл только в том случае, если определено множество возможных алгоритмов и задана вероятность использования каждого из них. Требования к криптографическим системам:
|



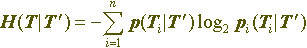
 H (T).
H (T).


