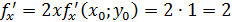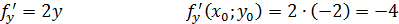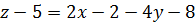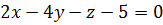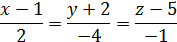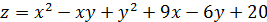Решение. Найдем частные производные первого порядка.
Найдем частные производные первого порядка.
Найдем частные производные второго порядка заданной функции:
Полный дифференциал 2-ого порядка функции
Задание №21. Найти производную
Решение
Вычисляем производную, считая
Выражая
Задание №31. Найти производные
Решение
Запишем неявно заданную функцию
Найдем частные производные первого порядка.
Тогда
Задание №41. Найти градиент функции
Решение
Вычислим частные производные и определим их значения в точке
Градиент функции
Найдем направляющие косинусы вектора
Производная по направлению равна
В точке
Задание №51. Написать уравнение касательной плоскости и нормали к заданной поверхности в точке
Решение Поскольку поверхность задана в виде
то уравнение касательной плоскости к указанной поверхности в заданной точке имеет вид:
Уравнение нормали имеет вид:
Вычислим частные производные функции
Тогда уравнение касательной плоскости принимает вид:
Уравнение нормали принимает вид:
Задание №61. Найти экстремум функции:
|
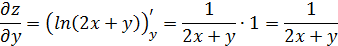
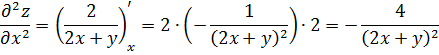
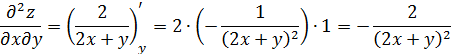
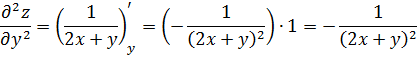
вычисляется по формуле:
неявно заданной функции:
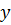функцией от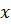 
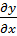получим искомую производную
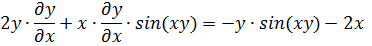
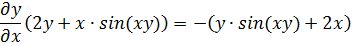
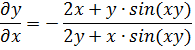
неявно заданной функции: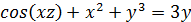
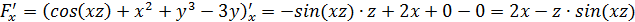
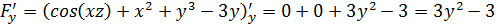
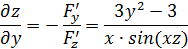
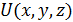в точке А и производную этой функции в точке А по направлению к точке В: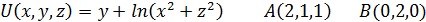
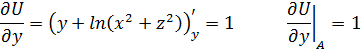
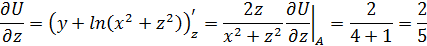
равен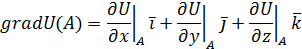
:
.
:
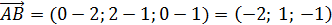
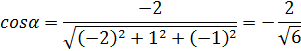
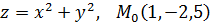
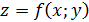
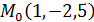