Фильтр с характеристикой Батерворта
Рабочая передаточная функция ослабление фильтра:
Рабочее ослабление фильтра Баттерворта:
Где:
N – порядок фильтра. 1) Нормализуем
2) Находим коэффициент неравномерности
3) Вычислим число реактивных элементов фильтра:
Округляем
4) Находим полюсы передаточной функции. Для ФНЧ Баттерворта (n = 3, k =1, 2, 3): S k
S 1 = - 0,467 + j0,808 S 2 = - 0,933 S 3 = - 0,467 - j0,808
5) Строим вспомогательные полиномы. Так как n = 3 - нечетное число, то составляем два вспомогательных полинома. Для первого выбираем корни с нечётными индексами: M(p) = (p – S1)(p – S3) = p2 + 0,93p + 0,8709
Для второго выбираем корни с чётными индексами: N(p) = (p – S2) = p + 0,933
6) Найдём коэффициент нормировки k и операторное входное сопротивление второй (правой) половины фильтра:
По методике ускоренного синтеза, раскладываем входное сопротивление в цепную дробь:
7) Из полученной цепной дроби выделяем нормированные элементы фильтра: LHOP =1,071 CHOP =1,071 RHOP =1 RHOP0 =
8) Этому разложению соответствует следующая схема правой половины фильтра:
9) Так как n = 3 нечетное, то выбираем левую схему фильтра симметричную правой половине:
10) Производим денормирование элементов и получаем окончательную схему фильтра: R0 = RHOP0 . RH = 1 . 50 = 50 Ом L1 = LHOP
C1 = C2 =
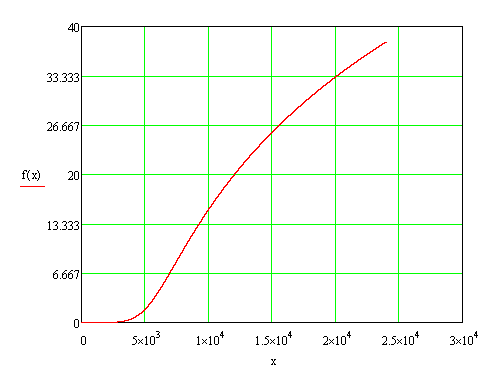
11) Строим график функции рабочего ослабления ФНЧ Баттерворта от частоты:
f
|
- коэффициент неравномерности в ПП;
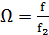- нормированная частота;
относительно 
:
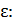
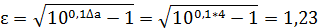
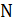до ближайшего целого большего числа n = 3.
= 
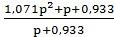
= 2,142 
Гн
Ф
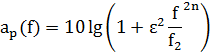
кГц
