Розглядається сталева прогонова будова пішохідного моста, прогін L = 6 м. В поперечному перерізі прогонова будова має 4 балки – двотаври №55. Вага 1 пог.м двотавра – q = 92 кг/м. Момент інерції двотавра – Iz=56000 см4. Модуль пружності сталі Еs = 2,1·106 кг/см2. Вага настилу і поручнів – p = 118 кг/м.
Визначити частоту і період вільних коливань з урахуванням сил опору слідуючи моделі системи з одним ступенем свободи.
Побудувати графік руху системи, якщо відомо, що поштовх викликав прогин у = 0,72yст, де yст – статичний прогин (від власної ваги прогонової будови). Коефіцієнт поглинання енергії (табл.1)  = 0,30.
= 0,30.
Розв’язок задачі наводиться нижче, в термінах MathCAD
| Коефіцієнт поглинання енергії
|
Вихідні дані (в кг та см)
Обчислення одиничного переміщення
| Повна вага прогонової будови:
|
| Прискорення вільного падіння:
|
| Статичний прогин прогонової будови:
|
Побудова графіку руху

Контрольні запитання до лекції 3
1. Дайте визначення поняття «Логарифмічний декремент»
2. Дайте визначення поняття «Коефіцієнт поглинання енергії»
3. Який зв'язок існує між коефіцієнтом поглинання енергії і логарифмічним декрементом коливань?
4. Наведіть диференційне рівняння руху системи з одним ступенем свободи з врахуванням її опору коливанням.
5. Наведіть форму загального розв’язку диференційного рівняння руху системи з одним ступенем свободи з врахуванням її опору коливанням.
6. ПРИКЛАД
Побудувати графік вільних коливань з урахуванням сил опору за даними прикладу, наведеного вище. Дослідити шляхом числового експерименту, як зміниться графік
а) при коефіцієнті поглинання енергії  = 0,20,
= 0,20,  = 0,40; Як змінюються при цьому частота і період вільних коливань
= 0,40; Як змінюються при цьому частота і період вільних коливань
б) визначити частоту і період вільних коливань при збільшенні власної ваги прогонової будови в 2 рази. Побудувати відповідний графік;
в) визначити частоту і період вільних коливань при збільшенні моменту інерції прогонової будови в 2 рази. Побудувати відповідний графік;
Общая характеристика интерфазного ядра. Функции ядра

 = 0,30.
= 0,30.
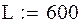
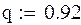





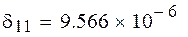


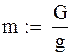
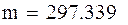
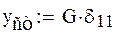




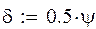






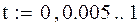


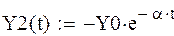

 = 0,20,
= 0,20, 


