Указания по выполнению заданий. Физико- технический факультет
Физико- технический факультет Кафедра информационных систем и технологий Буть С.В. Яничкин В.В. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ И ИНЖЕНЕРНАЯ ГРАФИКА ПРАКТИЧЕСКАЯ РАБОТА №3 ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПОВЕРХНОСТЬЮ для студентов дневной, вечерней и заочной форм обучения по специальностям
I-38.02.01 - информационно-измерительная техника, I-36.04.01- промышленная электроника, I-43.01.02 - электроэнергетические системы и сети, I-53.01.04 - автоматизация и управление энергетическими системами. Гродно 2010 ПРАКТИЧЕСКАЯ РАБОТА №3
ОПРЕДЕЛЕНИЕ ТОЧЕК ПЕРЕСЕЧЕНИЯ ПРЯМОЙ С ПОВЕРХНОСТЯМИ
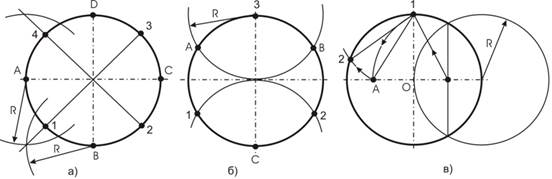
В данной работе решаются задачи по образному мышлению, т.е. при решении всех задач рассматриваются трехмерные объекты – поверхности. Все чертежи строятся по размерам в масштабе 1:1. Следует иметь в виду, что все поверхности выполнены из непрозрачного материала, поэтому при пересечении поверхности другими геометрическими образами проходящие внутри поверхности линии должны быть сплошными тонкими, как линии построения. При построении гранных поверхностей, таких как призма и пирамида, нужно уметь делить окружность на равные части (см. рис. 1), для построения проекции основания в виде правильного многоугольника вписанного в окружность заданного диаметра.
Рис. 1. Деление окружности на части: а) – на 4 и 8 частей; б) – на 3 и 6 частей; в) – на 5 и 10 частей (12 – пятая часть окружности, АО – десятая часть окружности) Задачи 1– 4
Определить точки встречи отрезка прямой AB с поверхностями: пирамиды, конуса, сферы и тора. Положение отрезка прямой АВ задано координатами.
Указания по выполнению заданий. Для выполнения задания необходимо изучить тему: «Построение точек пересечения прямой с поверхностями». По таблице 1 соответственно варианту определить данные для построения двух проекций поверхности. Дано: · О(50;45; 0) – центр окружности основания конуса, тора и окружности в которую вписано основание пирамиды; · центр сферы задан координатами (50: 45: 45), · d – диаметр сферы, нижнего основания тора, конуса и диаметр окружности в которую вписано основание пирамиды, · n – количество ребер пирамиды, · h – высота конуса и пирамиды, · диаметр верхнего основания тора 30мм, высота – 50мм, радиус образующей – 100мм. Таблица 1
ПОСТРОЕНИЕ ТОЧЕК ПЕРЕСЕЧЕНИЯ ПРЯМОЙ С ПОВЕРХНОСТЯМИ Построение точек пересечения прямой с поверхностью многогранника ( рис.2)
Рис.2 ны по линиям связи.
Построение точек пересечения прямой линии с конусом (рис. 3).
Чертеж конуса с проекциями вершин s, s' и прямой с проекциями a'b', ab приведен на рисунке 3, а. Для построения точек пересечения прямой и конуса используют вспомога-тельную плоскость. Плоскость, проходящая через вершину конуса и заданную прямую (плоскость P на рис., б), пересекает конус по образующим. Плоскость Р пересекает плоскость основания конуса по прямой DE, являющейся в данном случае горизонталью. Образующие, по которым плоскость P пересекает конус, определяются вершиной S и точками 1 и 2. На этих образующих и получаются точки M и N, в которых прямая пересекает поверхность конуса. На рисунке 3, а плоскость Р задана проекциями a'b', ab прямой AB и проекциями s'c', sc прямой, в данном случае горизонтальной, проведенной через вершину S, пересекающей прямую AB в точке С и параллельной плоскости основания конуса.
а б Рис. 3
Плоскость P пересекает плоскость основания конуса по прямой DE, параллельной SC. Построив проекции d' и d, проводим de ║ sc. Образующие, по которым плоскость P пересекает поверхность конуса, изображены лишь горизонтальными проекциями s–1 и s–2. В пересечении их с горизонтальной проекцией ab найдены горизонтальные проекции m и n точек пересечения, а по ним проекции m' и n'. На горизонтальной проекции отрезок прямой между точками М и N закрыт поверхностью конуса. На фронтальной проекции образующие S–1 и S–2 видимы. Следовательно, невидимый отрезок прямой AB находится только между проекциями m' и n'. Построение точки пересечения прямой линии со сферой (рис.4).
Зоны видимости участков прямой AB. На фронтальной проекции точки К (k') и L (l') видимы (они на передней полусфере). Следовательно, видимы в проекции лучей a'k' и lb' прямой. Между точками k' и l' сфера закрывает прямую. На горизонтальной проекции видимым является луч lb прямой (точка L находится на верхней полусфере). Слева от проекции l горизонтальная Рис.4 проекция прямой закрыта сферой.
Построение точки пересечения прямой линии с тором (рис.5). Построение выполняют, руководствуясь общим правилом. В качестве вспомо-гательной плоскости выбирают горизонтально-проецирующую плоскость R (Rh). Рис.5
Построение проекции линии пересечения вспомогательной плоскости с поверх-ностью тора начинают обычно с построения проекций характерных точек 1', 1 – крайней левой и 2', 2 – крайней правой и 3', 3 – высшей точки. Характерные точки линии пересечения: · это высшие и низшие точки по отношению к плоскости Н ближайшие и наиболее удаленные точки по отношению к наблюдателю; · точки, проекции которых отделяют видимую часть проекции линии пересечения от невидимой; · точки, лежащие в плоскости симметрии; · точки пересечения трех поверхностей – при наличии трех и более пересекающих-ся поверхностей. Для построения проекции 3' проводят горизонтальную проекцию параллели тора, касательной к плоскости R, и на ее фронтальной проекции находят проекцию 3'. Проекции промежуточных точек линии пересечения, например точки 4', 4, 5', 5, находят с помощью параллели, проходящей через точку с проекциями k', k. Построенные фронтальные проекции точек соединяют плавной кривой линией, точки пересечения которой m' и n' с фронтальной проекцией a'b' прямой AB являются фронтальными проекциями искомых точек пересечения прямой AB с поверхностью тора. По ним в проекционной связи строят горизонтальные проекции m и n точек пересечения. Невидимый отрезок MN прямой AB проведен штриховой линией.
|

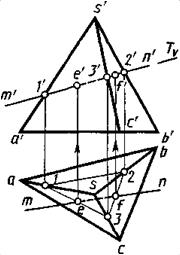 Построение точек пересечения прямой с поверхностью многогранника сводится к построению линии пересечения многогранника проецирующей плоскостью, в которую заключают данную прямую. На рисунке 4 приведено построение проекций e', e и f', f точек пересечения прямой с проекциями m'n', mn с боковыми гранями пирамиды. Пирамида задана проекциями s', s вершины и a'b'c', abc основания. Прямая MN заключена во вспомогательную фронтально-проецирующую плоскость T(Tv). Горизонтальные проекции e и f искомых точек построены в пересечении проекции mn с горизонтальными проекциями 1–2 и 2–3 отрезков, по которым плоскость T пересекает боковые грани пирамиды. Фронтальные проекции e' и f' определе-
Построение точек пересечения прямой с поверхностью многогранника сводится к построению линии пересечения многогранника проецирующей плоскостью, в которую заключают данную прямую. На рисунке 4 приведено построение проекций e', e и f', f точек пересечения прямой с проекциями m'n', mn с боковыми гранями пирамиды. Пирамида задана проекциями s', s вершины и a'b'c', abc основания. Прямая MN заключена во вспомогательную фронтально-проецирующую плоскость T(Tv). Горизонтальные проекции e и f искомых точек построены в пересечении проекции mn с горизонтальными проекциями 1–2 и 2–3 отрезков, по которым плоскость T пересекает боковые грани пирамиды. Фронтальные проекции e' и f' определе-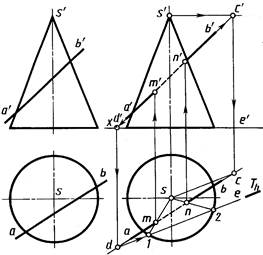
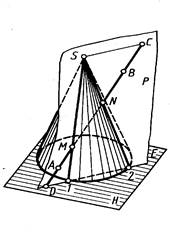
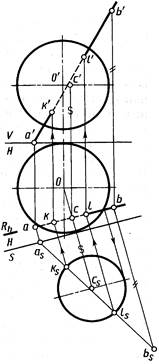 Используя вспомогательную секущую плоскость, проходящую через данную прямую, получают окружность. Искомые точки К и L получаются при пересечении этой окружности прямой линией. На рисунке 4 построения выполнены способом перемены плоскостей проекций. Дополнительную плоскость проекций S выбирают параллельной вспомогательной, например горизонтально-проецирующей плоскости R (Rh). B этом случае линия пересечения вспомогательной плоскости с поверхностью сферы проецируется на плоскость S в окружность с центром cs, с которой проекция asbs прямой линии пересекается в точках ks и ls. По ним строят горизонтальные k и l и фронтальные k' и l' проекции искомых точек пересечения.
Используя вспомогательную секущую плоскость, проходящую через данную прямую, получают окружность. Искомые точки К и L получаются при пересечении этой окружности прямой линией. На рисунке 4 построения выполнены способом перемены плоскостей проекций. Дополнительную плоскость проекций S выбирают параллельной вспомогательной, например горизонтально-проецирующей плоскости R (Rh). B этом случае линия пересечения вспомогательной плоскости с поверхностью сферы проецируется на плоскость S в окружность с центром cs, с которой проекция asbs прямой линии пересекается в точках ks и ls. По ним строят горизонтальные k и l и фронтальные k' и l' проекции искомых точек пересечения.



